Man kann Flächen genau beschreiben. Du kennst schon spezielle Flächen wie das Dreieck oder das Quadrat. Was macht diese und andere Flächen so unverwechselbar?

§
© Digitale Lernwelten GmbH
Flächen richtig beschreiben
Was sind Flächen?
§
© Digitale Lernwelten GmbH
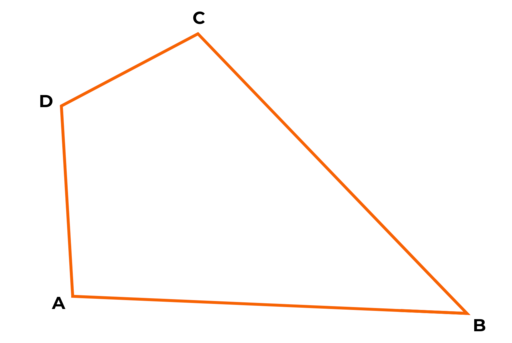
Flächen können eben oder gewölbt sein. Jede Fläche ist von Linien begrenzt.
Sie ragen nicht in den Raum hinein.
Dort, wo zwei Linien aufeinandertreffen, entsteht eine Ecke. Ecken werden mit Großbuchstaben und entgegen dem Uhrzeigersinn benannt.
Mehrere Flächen können einen Körper bilden.
Hier kannst du ausprobieren, wie verschiedene Körper durch Flächen gebildet werden:
- Wähle rechts den Würfel oder den Quader. Du kannst auch einstellen, wie lang die Kante a sein soll.
- Ziehe den Regler nach unten oder greife einen der Eckpunkte, um den Körper zu falten.
§
© Digitale Lernwelten GmbH
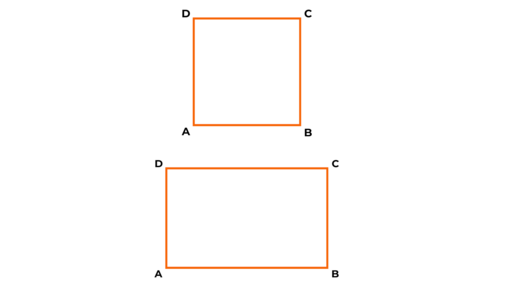
Manche Flächen haben spezielle Formen.
Flächen können wir genau beschreiben.
Flächen mit besonderen Formen: das Quadrat
Um die Eigenschaften des Quadrats und anderer besonderer Flächen (auch Figuren genannt) besser zu verstehen, lernen wir zuerst einige Begriffe anhand von Geraden. Die Geraden stellen dabei die Lage der Seiten dar.

§
© Digitale Lernwelten GmbH
- Alle Seiten sind gleich lang.
Zwei Seiten im Quadrat liegen entweder parallel oder senkrecht zueinander.
Benachbarte Seiten stehen senkrecht zueinander und schließen einen rechten Winkel ein.
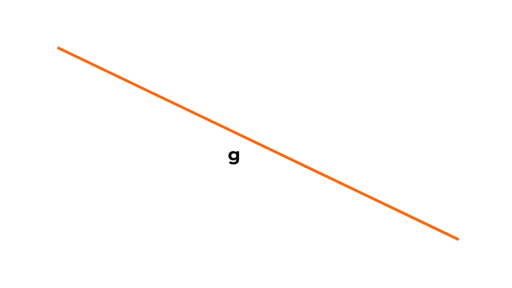
Die Gerade
§
© Digitale Lernwelten GmbH
Anstatt Seiten können wir auch Geraden betrachten.
Geraden sind geometrische Figuren, die unendlich lang sind.
Sie haben weder Anfang noch Ende.
Man bezeichnet Geraden mit einem kleinen Buchstaben.
§
© Digitale Lernwelten GmbH
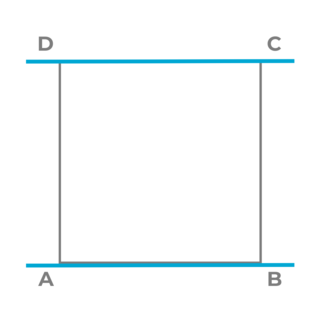
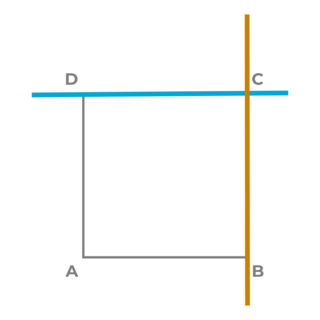
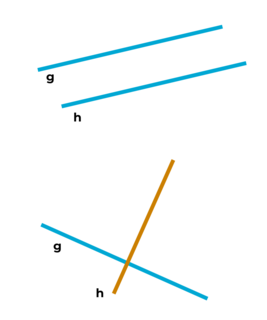
Zwei Geraden können wie die Seiten in einem Quadrat
- parallel zueinander liegen.
§
© Digitale Lernwelten GmbH
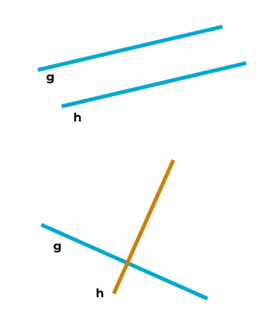
senkrecht zueinander liegen.
§
© Digitale Lernwelten GmbH
„Die Gerade g ist parallel zur Geraden h“
Kurzschreibweise: g II h
„Die Gerade g ist senkrecht zur Geraden h“
Kurzschreibweise: g ⊥ h
Anwendung
Anwendung
§
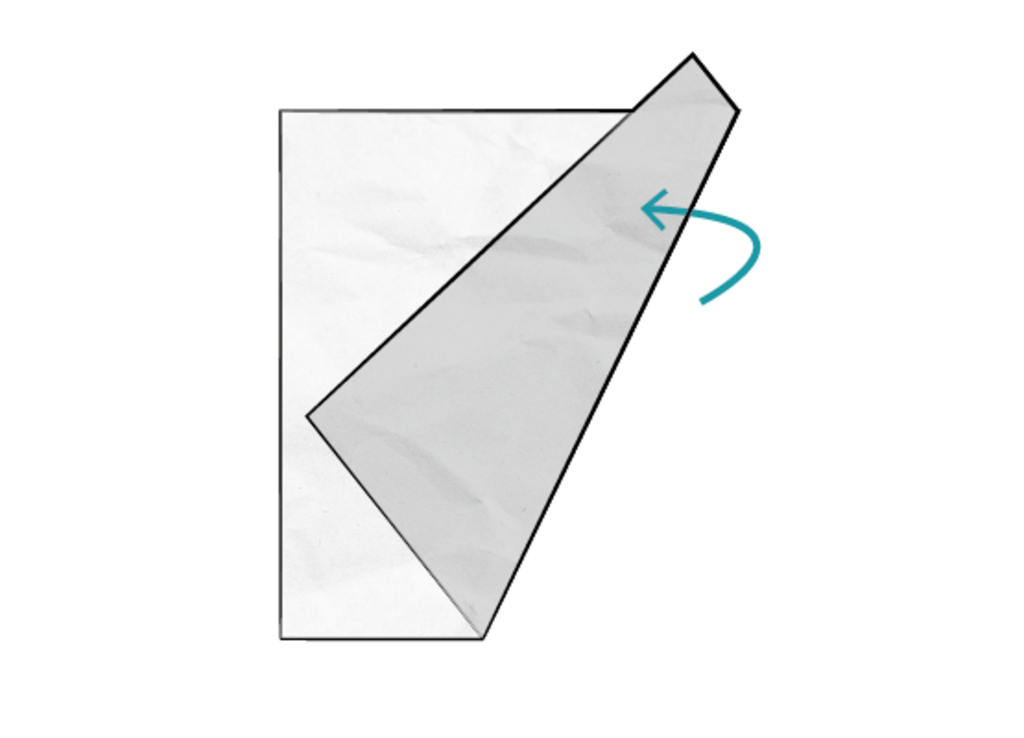
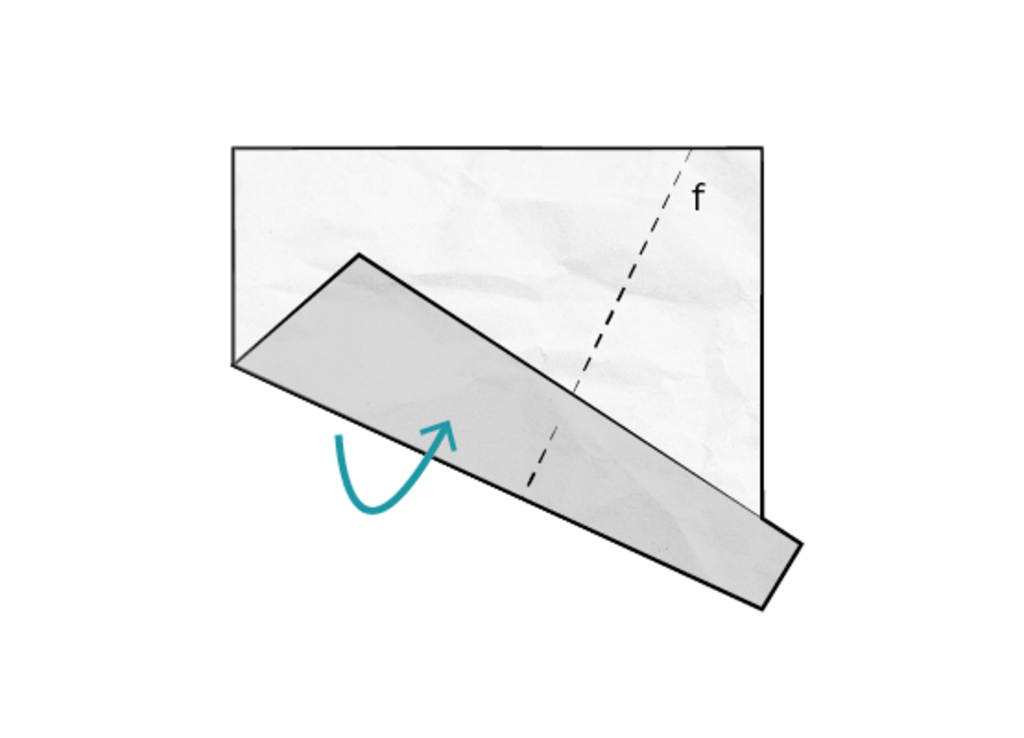
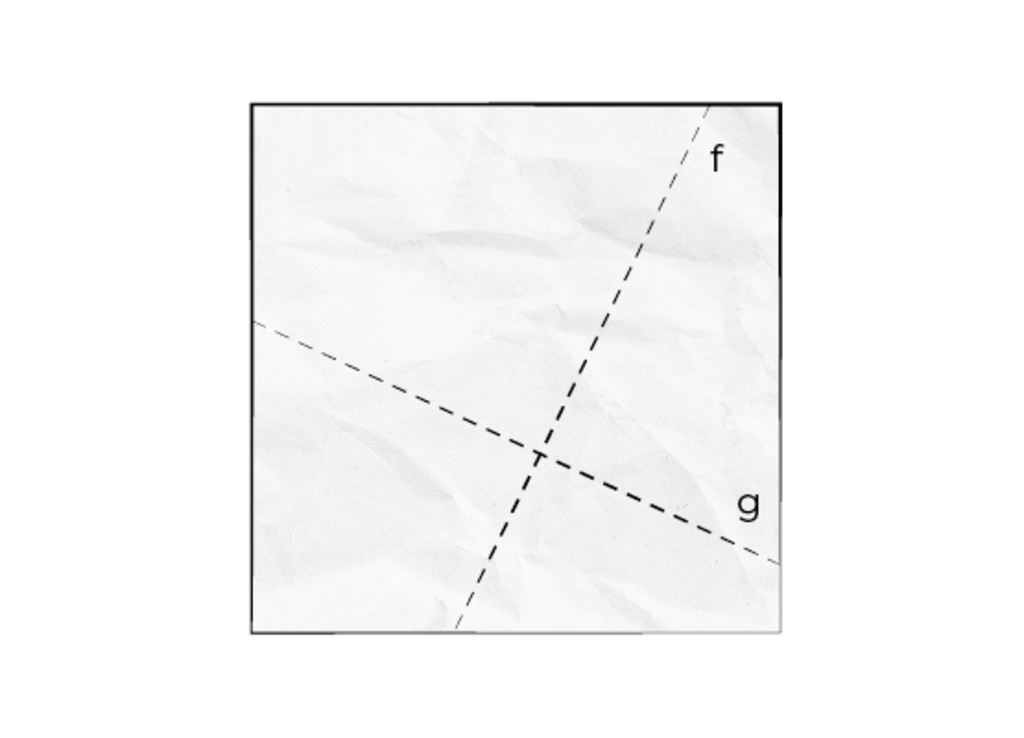
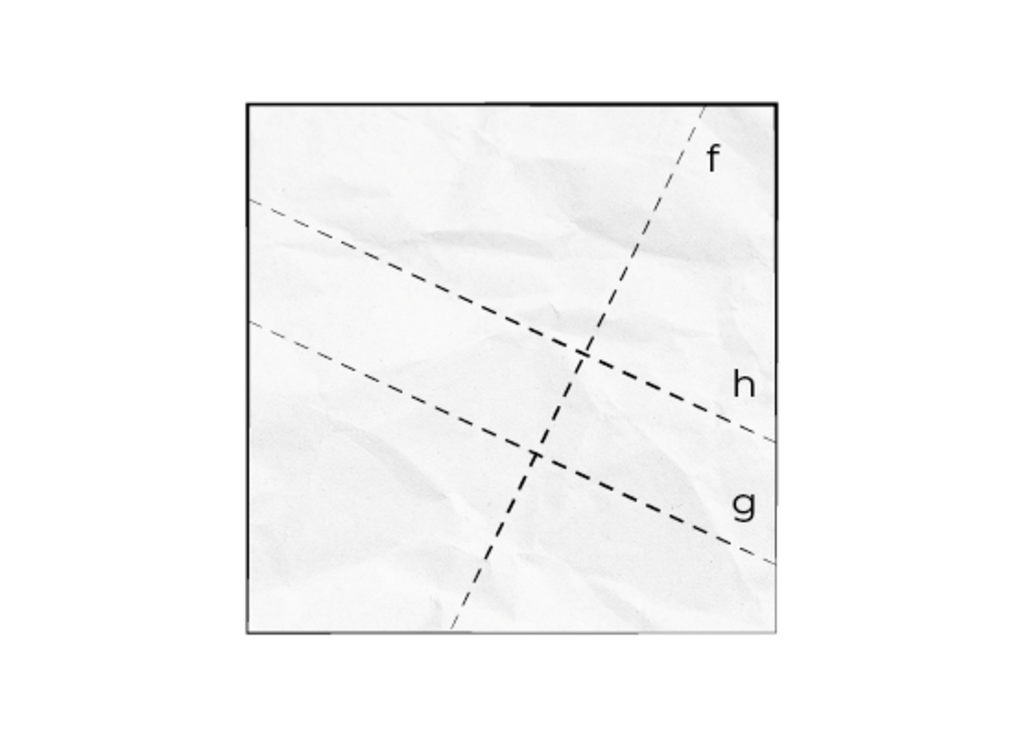
Cc4 BY NC SA 1) Falte das Quadrat mit einem beliebigen Knick.

§
§
§
§
§
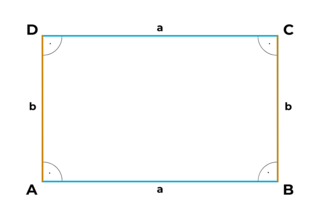
Flächen mit besonderen Formen: das Rechteck
§
© Digitale Lernwelten GmbH
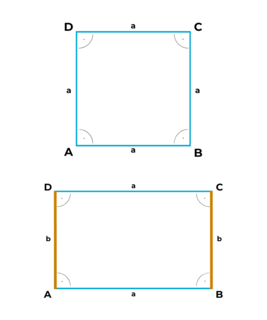
- Gegenüberliegende Seiten sind immer parallel.
- Gegenüberliegende Seiten sind immer gleich lang.
- Nachbarseiten sind immer senkrecht zueinander.
- Jede Seite wird mit einem Kleinbuchstaben bezeichnet.
- Die Figur hat 4 rechte Winkel.
§
© Digitale Lernwelten GmbH
Das Quadrat ist ein Rechteck, bei dem alle Seiten gleich lang sind.
Aufgabe
Miss die Seitenlängen der Formen und trage sie in die Felder ein.
Download
Miss die Seitenlängen der Formen und trage sie in die Felder ein.
Download
Ordne die Formen, Dinge und Aussagen richtig zu!
Merkwissen für deine Notizen
Eigenschaften von Flächen
§
© Digitale Lernwelten GmbH
Was sind Flächen?
- Flächen sind eben oder gewölbt und von Linien begrentz, die man Seiten nennt.
- Eckpunkte werden mit Großbuchstaben benannt, Seiten mit Kleinbuchstaben.
Flächen ragen nicht in den Raum hinein.
Körper werden von Flächen begrenzt.
Manche Flächen haben besondere Formen.
§
© Digitale Lernwelten GmbH
Flächen mit besonderen Formen
Quadrat
Rechteck
§
© Digitale Lernwelten GmbH
Besondere Lage von Geraden zueinander
parallel (g II h)
senkrecht (g ⊥ h)
Winkel
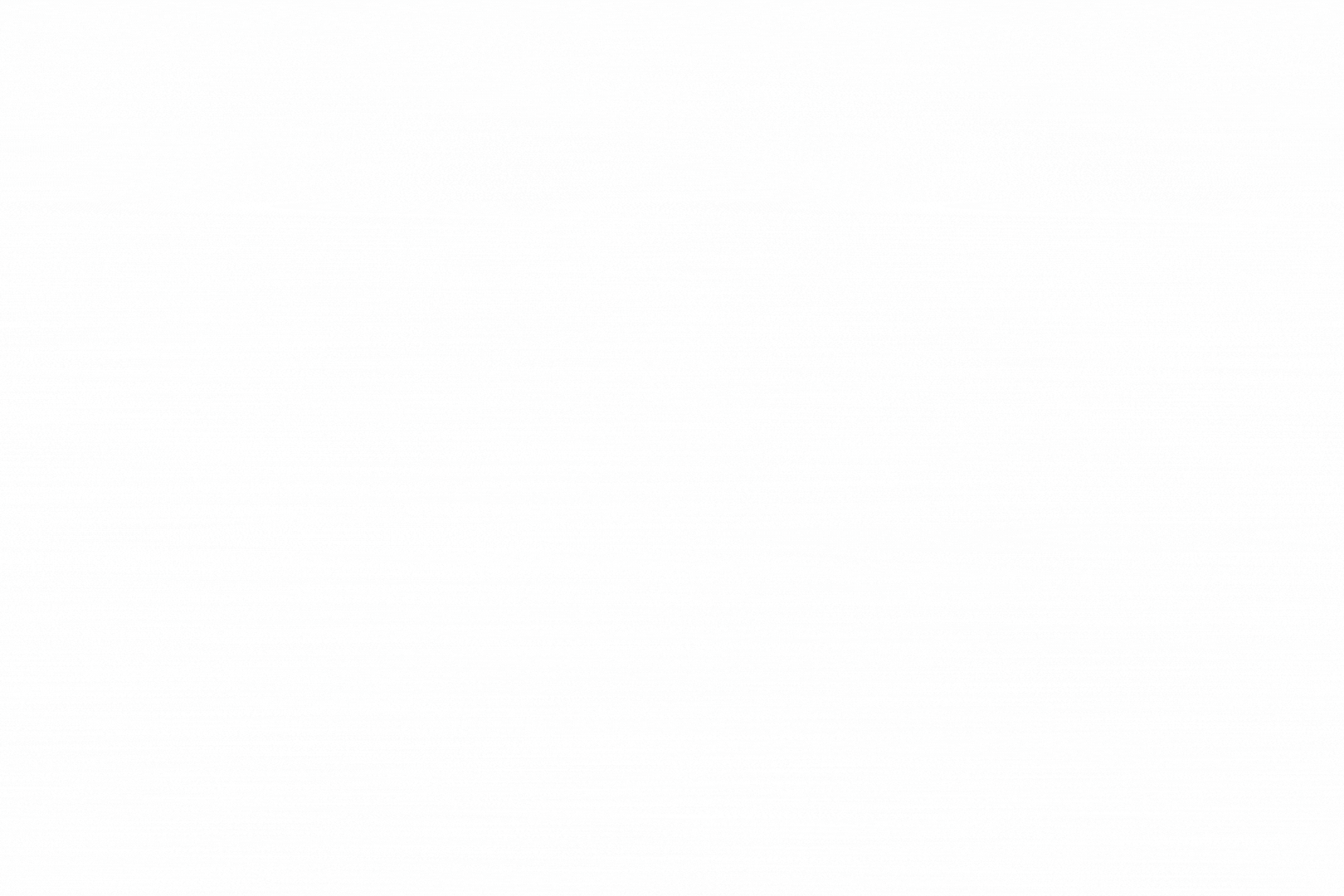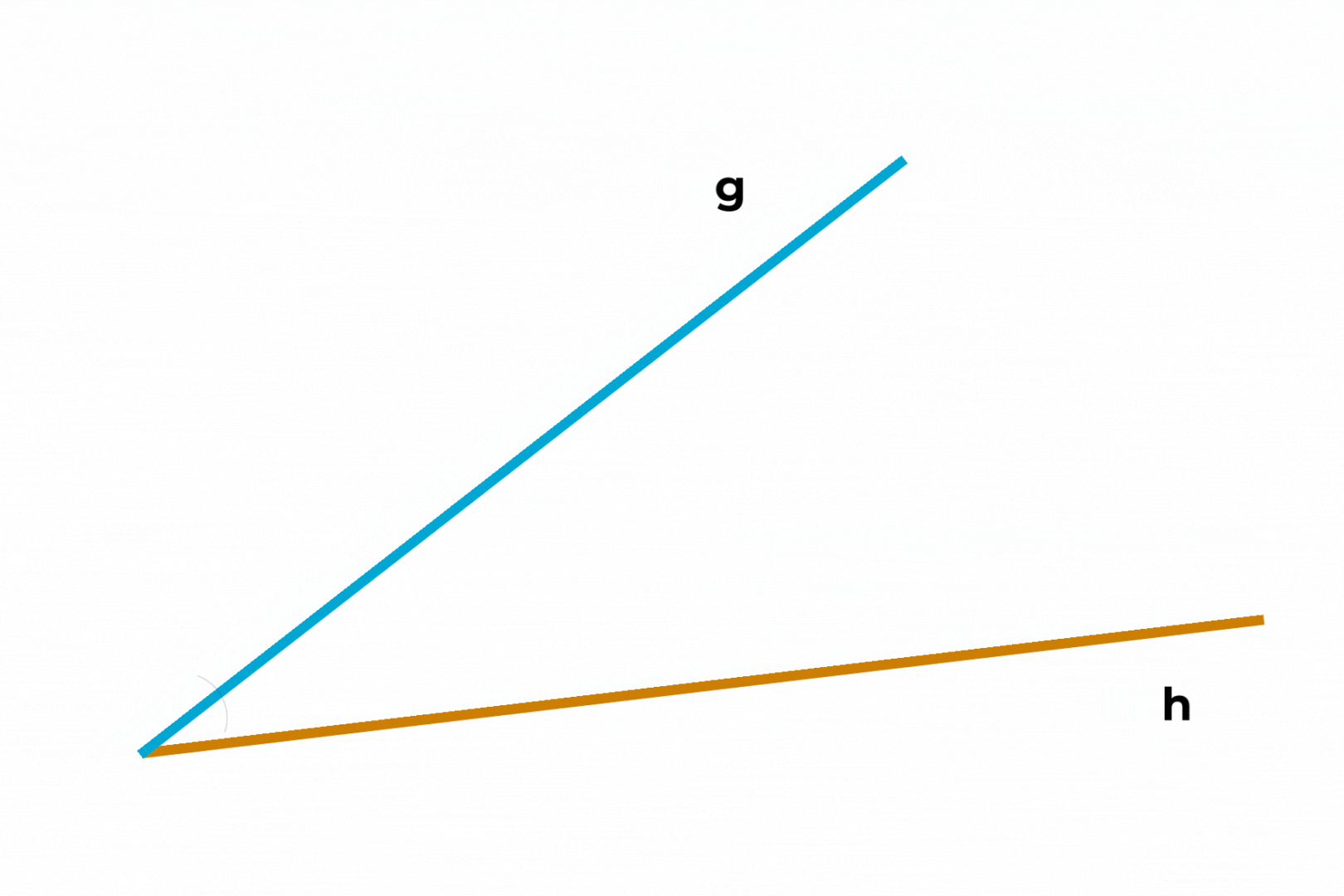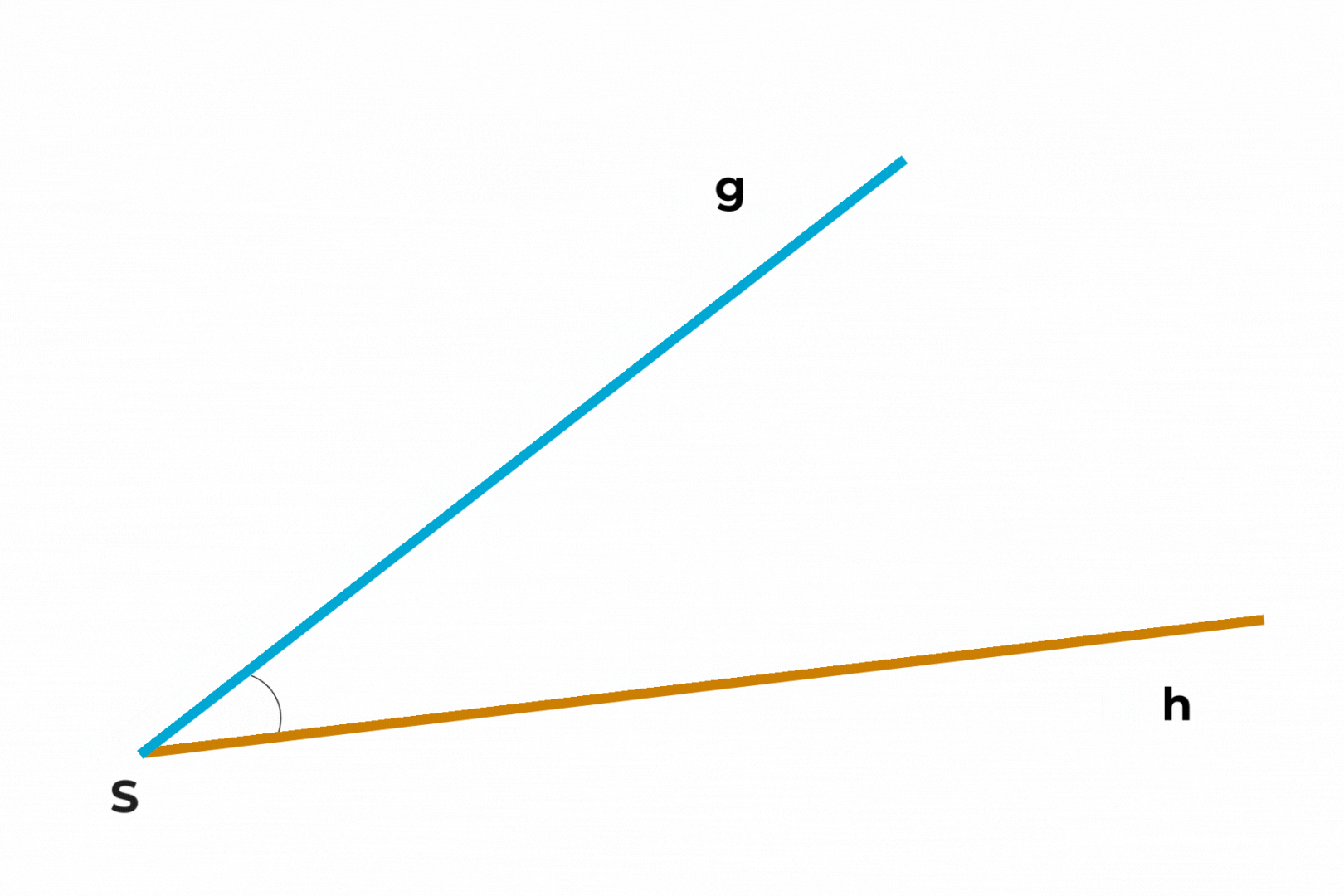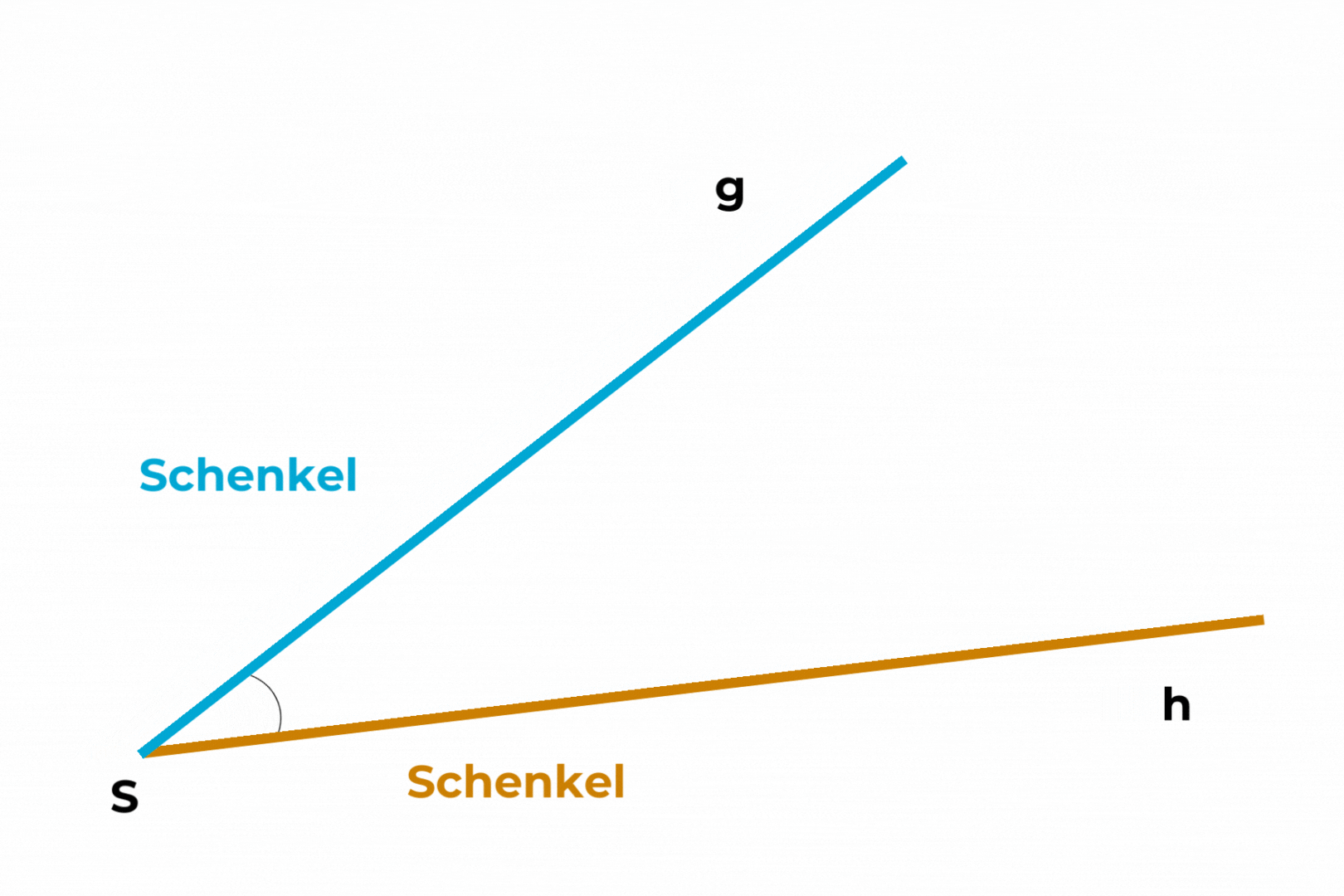
§
© Digitale Lernwelten GmbH
Ein Winkel entsteht dort, wo sich zwei Geraden treffen.
Wenn Geraden einen Anfangspunkt haben, nennt man sie Halbgeraden oder Strahlen.
Der Punkt, an dem sich die beiden Halbgeraden treffen, heißt Scheitelpunkt.
Die Halbgeraden, die den Winkel begrenzen, werden Schenkel genannt.
Winkel messen
Winkel misst man in Grad.
Es gibt besondere Winkelgrößen, die du jetzt kennenlernst.
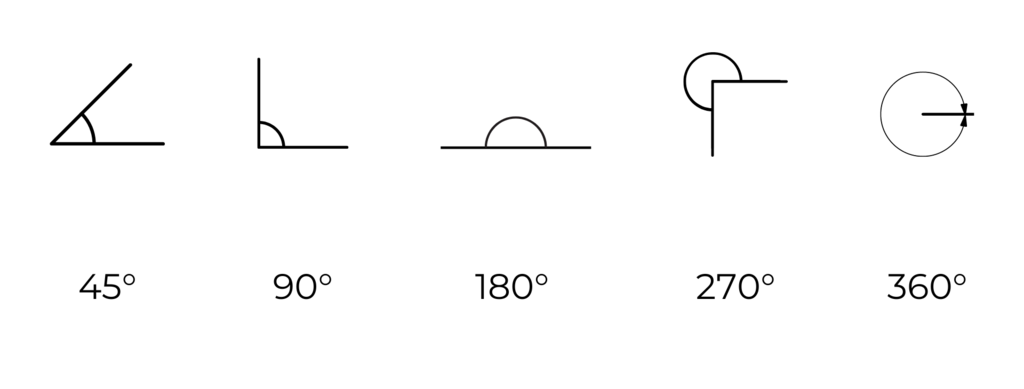
§
© Digitale Lernwelten GmbH
Aufgabe
- Klicke auf „Start“. Oben rechts erscheint nun eine Gradzahl.
- Bewege die blaue Gerade, um den Winkel auf die angegebene Größe einzustellen.
- Klicke auf „Prüfen“ und sieh nach, wie gut du geschätzt hast.
- Klicke auf „Weiter“ und wiederhole die Übung 10 mal.
- Ziehe am roten Punkt, um den Winkel möglichst genau auf die vorgegebene Größe einzustellen.
- Klicke auf „Prüfen“ und sieh nach, wie gut du geschätzt hast.
- Klicke auf „Neue Aufgabe“ und wiederhole die Übung 10 mal.
- Sieh dir den Winkel genau an und schätze, wie viel Grad er groß ist.
- Trage die Zahl in das Feld unten links ein und drücke Enter.
- Klicke auf „Lösung anzeigen“ um nachzusehen, wie gut du geschätzt hast.
- Klicke auf „neuer Winkel“ und wiederhole die Übung 10 mal.
§
© Digitale Lernwelten GmbH
Merkwissen für deine Notizen

§
Urheber: Digitale Lernwelten GmbH
Winkel
Winkel messen mit dem Geodreieck
0-Markierung des Geodreiecks am Scheitelpunkt anlegen.
Grundkante des Geodreiecks am Schenkel ausrichten.
Die richtige Skala wählen (an der Grundkante fängt die Skala mit 0° an).
Winkelgröße ablesen.
Übungen
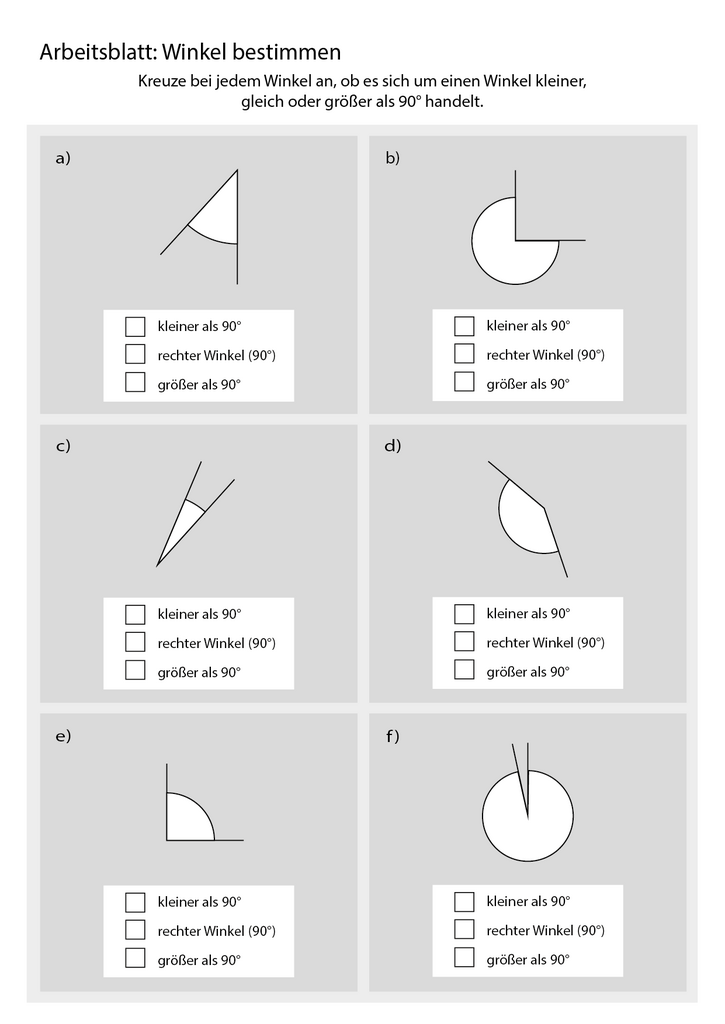
§
© Digitale Lernwelten GmbH
Entscheide, welche Winkel kleiner, größer oder gleich 90° sind. Prüfe mit dem Geodreieck. Miss die Winkel nach!
Download
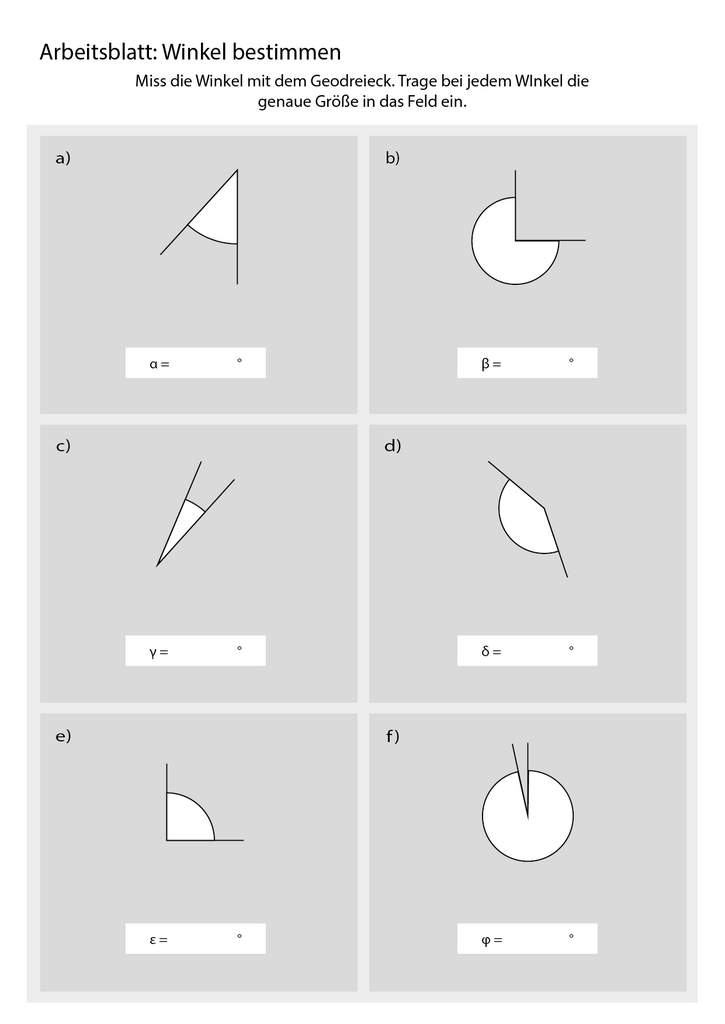
§
© Digitale Lernwelten GmbH
Miss die Winkel möglichst genau.
Download
Winkel bezeichnen mit griechischen Buchstaben

§
© Digitale Lernwelten GmbH
Du hast bereits gelernt, dass die Ecken einer Fläche mit Großbuchstaben (A, B, C, ...) und die Seiten einer Fläche mit Kleinbuchstaben (a, b, c, ...) bezeichnet werden.
Die Winkel, die zwischen den Seiten entstehen, werden mit griechischen Buchstaben benannt.
Hier kannst du dir die Aussprache der griechischen Buchstaben α, β, γ und δ anhören.
Merkwissen für deine Notizen

§
Urheber: Digitale Lernwelten GmbH
Winkel werden mit griechischen Buchstaben bezeichnet.
Alpha α
Beta β
Gamma γ
Delta δ
Winkelbezeichnungen am Dreieck
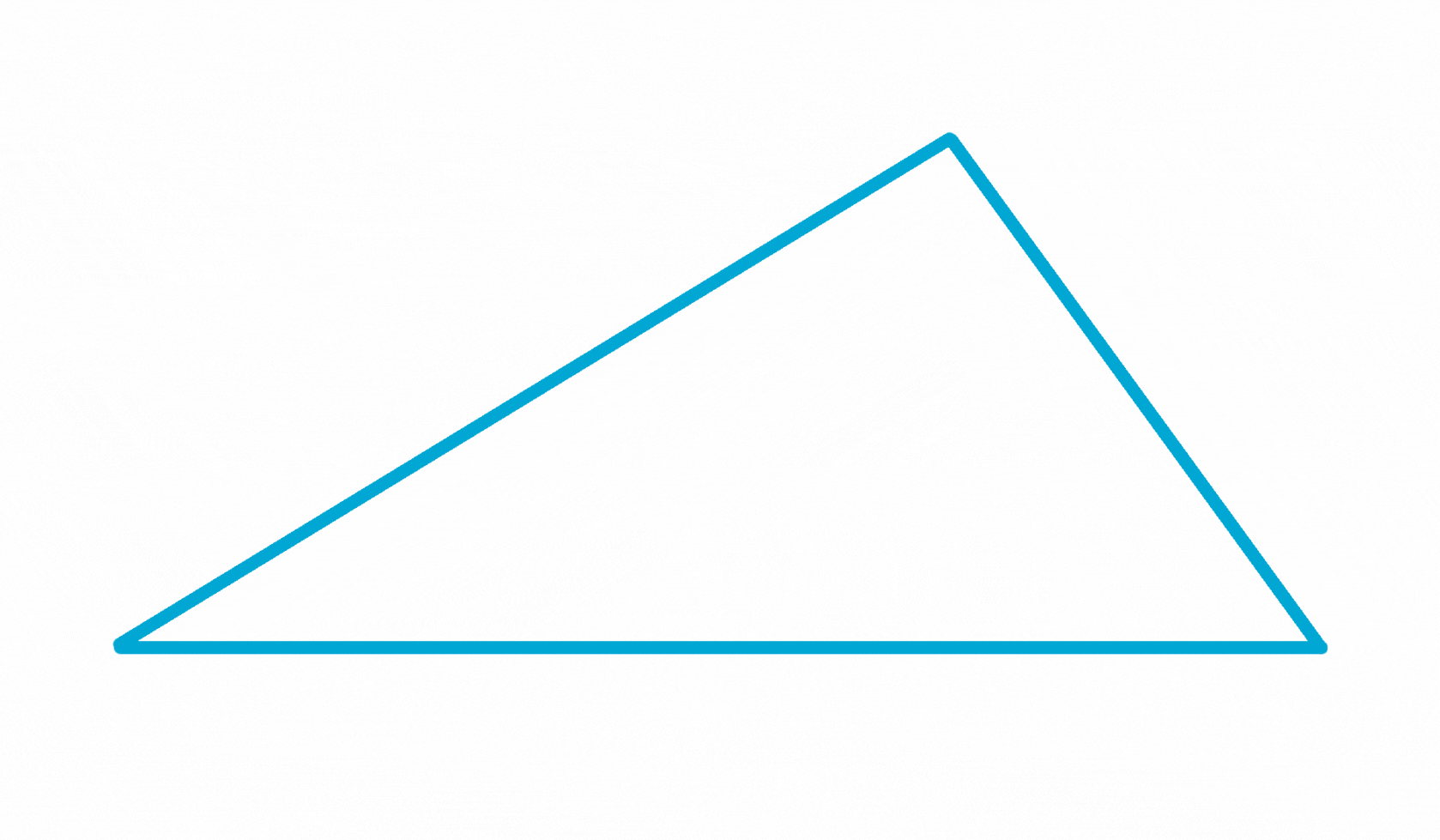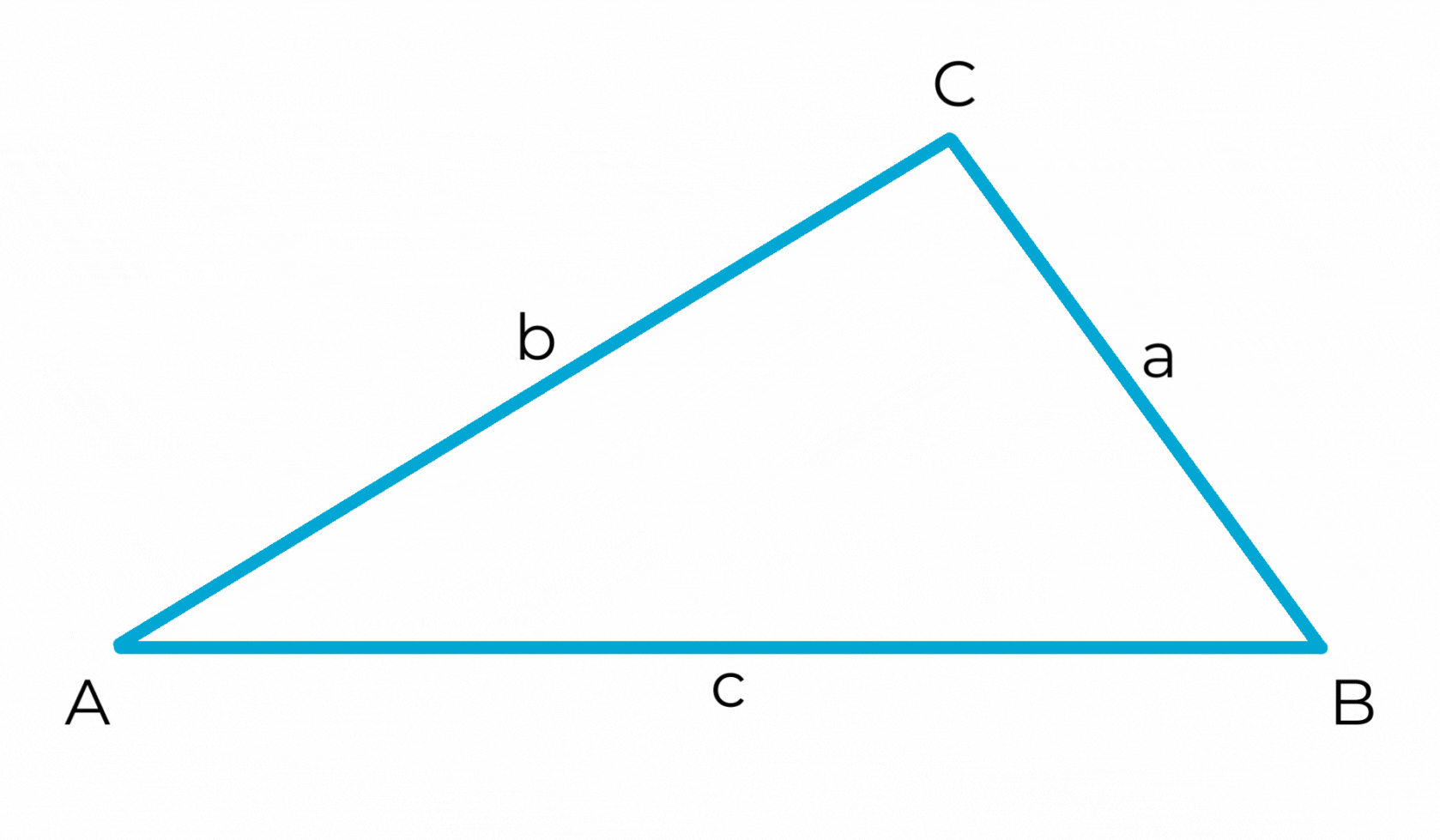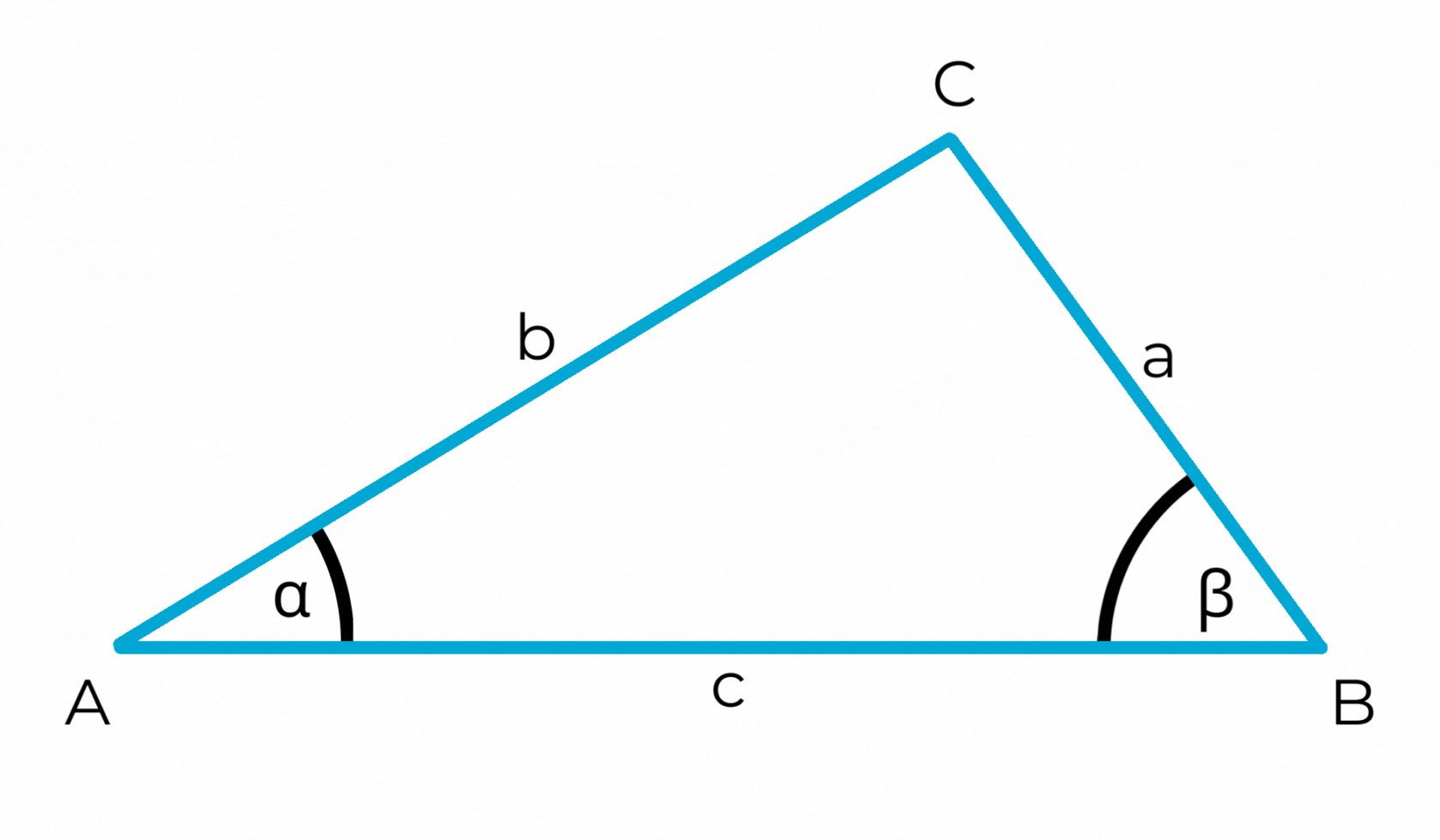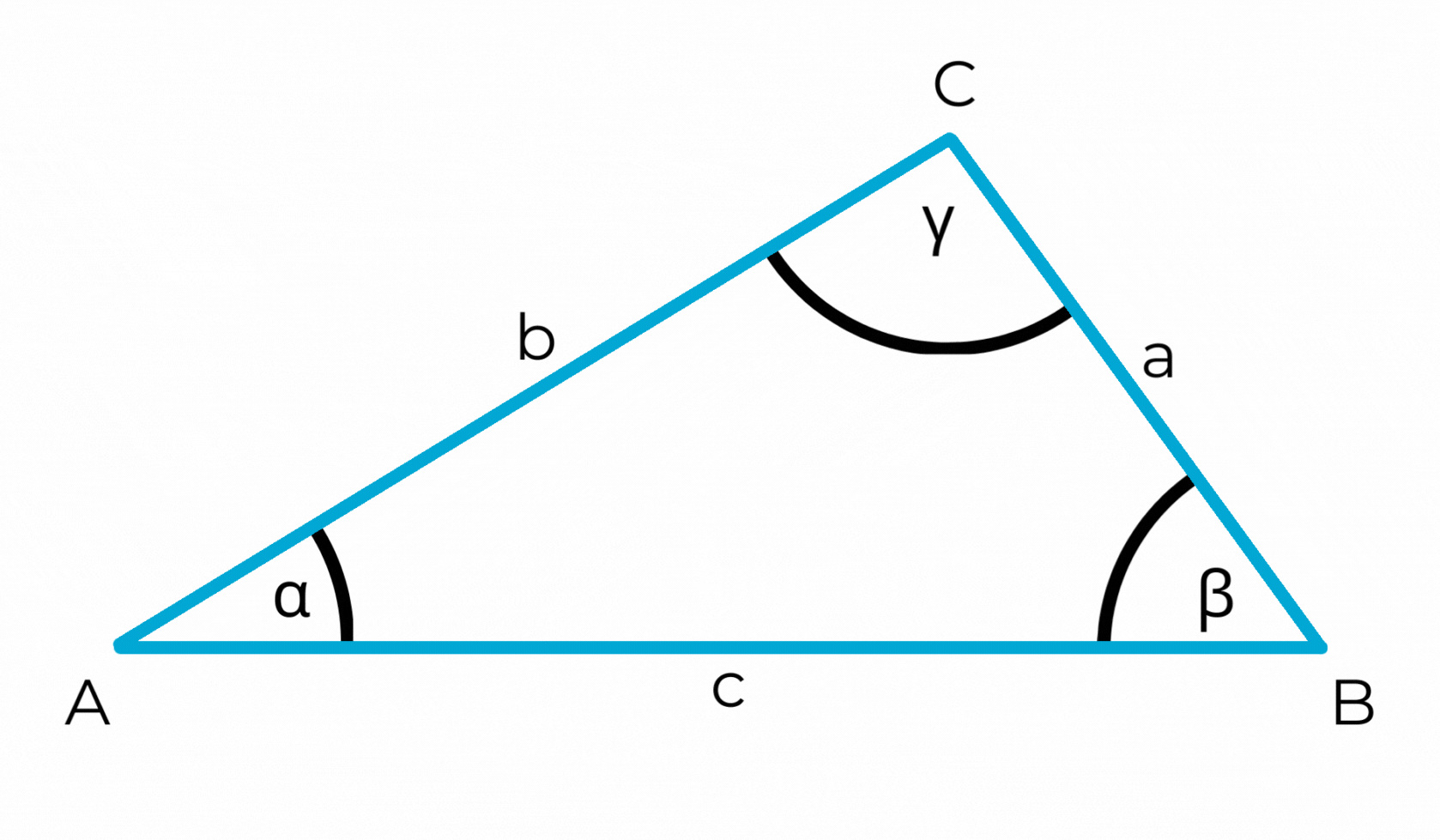
Du hast bereits gelernt, wie die Eckpunkte einer Fläche beschriften werden: mit Großbuchstaben.
Bei einem Dreieck nimmt man normalerweise die Buchstaben A, B und C. Die Ecken werden dabei entgegen dem Uhrzeigersinn benannt.
Die Winkel werden mit griechischen Kleinbuchstaben bezeichnet, normalerweise α, β und γ. Diese schreibt man in die Winkelbögen.
§
© Digitale Lernwelten GmbH
Beschrifte die Ecken, Seiten und Winkel der Dreiecke!
Winkelarten
Winkelarten
Winkelarten (Winkel Modul Winkelarten Video Nr. 3) und die Aufgaben darin
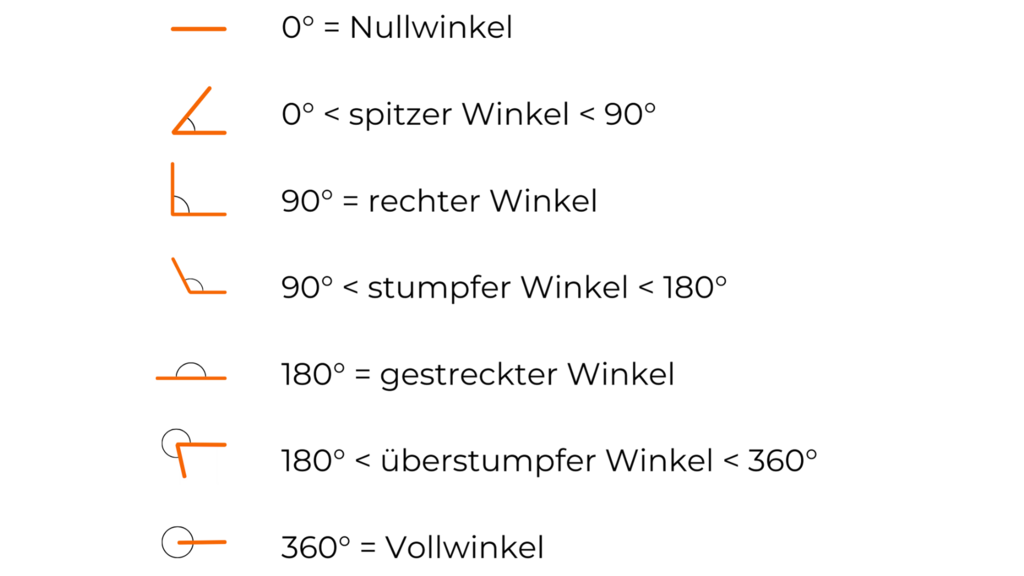
§
© Digitale Lernwelten GmbH
Mit dieser Übung kannst du dein Wissen über Winkel festigen. Ziehe das rote Kreuz und achte dabei darauf, wie die dabei entstehenden Winkel bezeichnet werden.
Ordne nun die Bezeichnungen richtig zu. Wenn du dir nicht sicher bist, kannst du die vorherige Übung nutzen, um nachzuschauen.
Merkwissen für deine Notizen

§
Urheber: Digitale Lernwelten GmbH
Eigenschaften von Winkeln
Schneiden sich zwei Geraden, entsteht dazwischen ein Winkel.

§
© Digitale Lernwelten GmbH
Die beiden entstehenden Strahlen werden Schenkel genannt.
Der Winkel wird mit einem griechischen Buchstaben bezeichnet (α - Alpha)
Die Winkel in einem Dreieck werden entgegen dem Uhrzeigersinn und entsprechend der mit Großbuchstaben bezeichneten Eckpunkte benannt (α, β, γ - Alpha, Beta, Gamma)
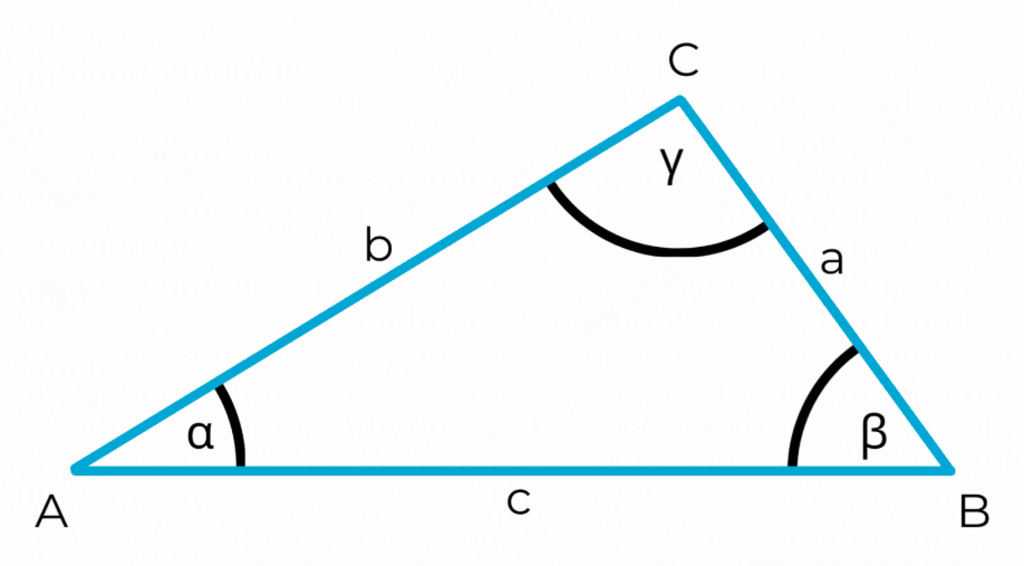
§
© Digitale Lernwelten GmbH
Winkel sind abhängig von ihrer Größe in folgende Winkelarten eingeteilt:

§
© Digitale Lernwelten GmbH
§
© Digitale Lernwelten GmbH
Super, du hast nun auch das dritte Kapitel geschafft! Hier geht es zum letzten Kapitel.