
§
© Digitale Lernwelten GmbH, erstellt mit Canva
Experiment: geneigte Ebene | SEK 2

§
Geeignete Ebene und freier Fall
Hier wirst du dich detailliert mit der gleichmäßig beschleunigten Bewegung auseinandersetzen.
Analyse von Messwerten
In diesem Modul erwarten dich spannende Experimente zum nachbauen.
Bevor du anfängst, überprüfe mit dieser Checkliste, ob du das notwendige Basiswissen parat hast:
- Ich verstehe den Unterschied zwischen der Durchschnittsgeschwindigkeit und der Augenblicksgeschwindigkeit.
- Ich kann das s(t)-Diagramm (Weg-Zeit-Diagramm) und das v(t)-Diagramm (Geschwindigkeit-Zeit-Diagramm) für eine gleichförmige Bewegung zeichnen.
- Ich weiß, wie man die Bewegungsgleichung für die Berechnung des Weges s in Abhängigkeit von der Zeit t aufschreibt und kann sie in Aufgaben anwenden.
Wenn du eine Lücke in deinem Wissen findest, ist das kein Problem. Nutze deine Unterrichtsnotizen, das Schulbuch oder sprich mit deiner Lehrkraft. Auch anhand der folgenden Merkkästen kannst du dein Wissen auffrischen und erweitern.
Unterscheidung Durchschnitts- und Augenblicksgeschwindigkeit
Unterscheidung Durchschnitts- und Augenblicksgeschwindigkeit
Tom radelt auf einem Teil des Mainradweges, und zwar von Würzburg nach Gemünden. Diese Strecke ist s=43 km lang. Ohne Pausen hat er dafür t=135 Minuten gebraucht.
Wenn wir daraus seine Geschwindigkeit berechnen, bekommen wir seine Durchschnittsgeschwindigkeit:
v = s/t = 43 km : 135 min = 43000 m : 8100 s ≈ 5,3 m/s
Tipp: Um diese Geschwindigkeit in km/h umzurechnen, multipliziere sie mit 3,6. (Das bedeutet: 5,3 m/s = 19,1 km/h)
Während seiner Fahrt wird Tom manchmal schneller und manchmal langsamer sein. Wenn Tom seine Geschwindigkeit zu einem bestimmten Zeitpunkt wissen möchte, könnte er ein Tachometer verwenden. Die Geschwindigkeit, die zu einem bestimmten Zeitpunkt gemessen wird, nennt man Augenblicksgeschwindigkeit.
s(t)- und v(t)-Diagramm der gleichförmigen Bewegung
s(t)- und v(t)-Diagramm der gleichförmigen Bewegung
§
Urheber: Digitale Lernwelten GmbH
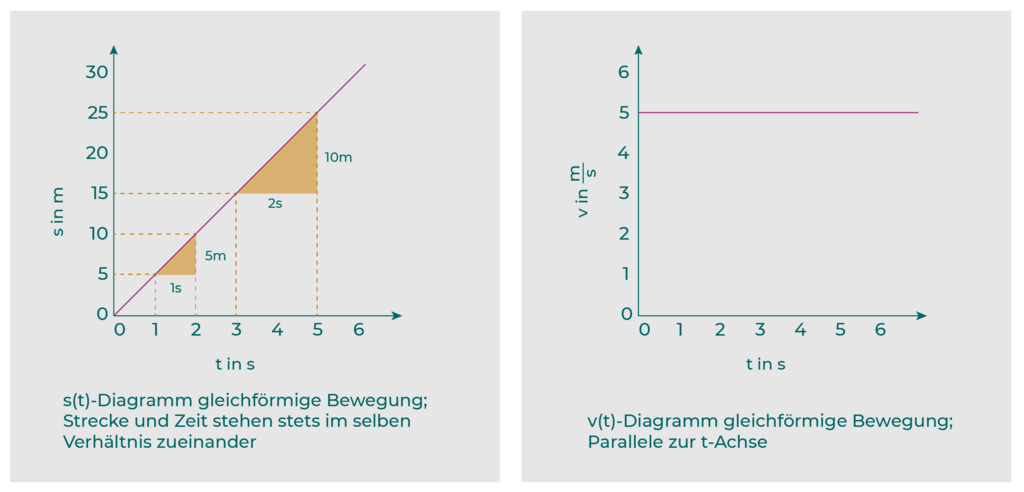
s(t)-Diagramm gleichförmige Bewegung; Strecke und Zeit stehen stets im selben Verhältnis zueinander
Für Bewegungen mit konstanter Geschwindigkeit gilt: s~t. Im s(t)-Diagramm ist somit eine Ursprungsgerade zu sehen, und das v(t)-Diagramm zeigt eine Parallele zur t-Achse.
Bewegungsgleichungen der gleichförmigen Bewegung
Bewegungsgleichungen der gleichförmigen Bewegung
Je steiler die Ursprungsgerade im s(t)-Diagramm ist, desto höher ist die Geschwindigkeit des Objektes. Die Geschwindigkeit ist also die Proportionalitätskonstante. Es gilt:
s(t) = v * t und v(t) = konst.