Zuerst führst du einen mehrstufigen Zufallsversuch durch.

§
© Digitale Lernwelten GmbH auf Basis von Canva
Mehrstufige Zufallsversuche
Aufgabe: Hinführung 1

§
Urheber: Digitale Lernwelten GmbH auf Basis von Canva
Nimm eine Münze und wirf sie insgesamt dreimal hintereinander. Bei jedem Wurf kann entweder Wappen (W) oder Zahl (Z) vorkommen.
Schreibe die Ergebnisse deines Zufallsversuchs in das Textfeld.
Wenn zu zum Beispiel erst Zahl, dann Wappen und dann wieder Zahl geworfen hast, schreibst du Z-W-Z.
Mögliche Ergebnisse
Mögliche Ergebnisse
Z-Z-Z oder Z-Z-W oder Z-W-W oder W-Z-W und so weiter ...
Aufgabe: Hinführung 2
Wiederhole den Versuch von gerade fünfmal. Schreibe jedes Mal das Ergebnis auf.
Mögliche Ergebnisse
Mögliche Ergebnisse
Z-W-Z; W-W-Z; Z-Z-Z; W-W-W; W-W-Z
oder
W-Z-Z; Z-Z-W; W-Z-W; Z-Z-Z; W-W-W
usw.
Hast du alle verschiedenen Möglichkeiten erzielt? Wäre es nicht toll, wenn du alle Optionen auf einen Blick sehen könntest?
Das kannst du - mit einem Baumdiagramm!
Hier siehst du Schritt für Schritt, wie das geht. Dann kannst du in der interaktiven Übung das Baumdiagramm zu folgendem mehrstufigen Zufallsversuch ausfüllen:
Eine Münze wird dreimal hintereinander geworfen.
So sieht ein Baumdiagramm aus. Jeder Wurf der Münze wird als „Astgabelung“ nach rechts ergänzt.
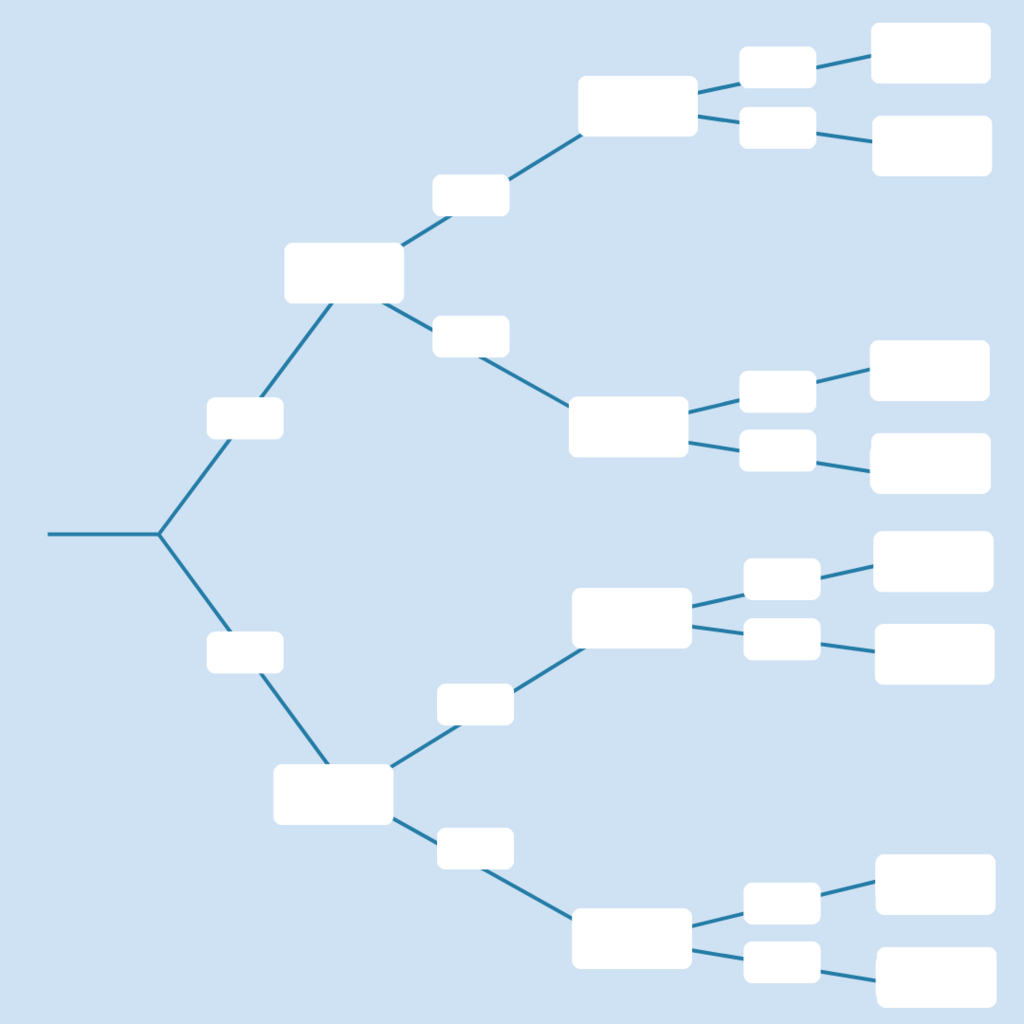
§
In die großen Felder des Baumdiagramms trägt man die Ergebnisse ein, z. B. das Ergebnis W-Z-Z.

§
Jetzt bist du dran! Ergänze die jeweiligen Ergebnisse in den großen Feldern.
Schreib jetzt die Wahrscheinlichkeiten für jedes Ergebnis in die kleinen Kästchen.
Du weißt schon, dass die Wahrscheinlichkeit, beim ersten Wurf eine Zahl (Z) zu bekommen, 1/2 ist. Wie stehen die Chancen bei den anderen Würfen?
Vervollständige die anderen kleinen Kästchen mit den passenden Wahrscheinlichkeiten!
Merkwissen für deine Notizen
Sieh dir das folgende Video an und notiere dir die wichtigsten Punkte!
zum Üben
Aufgabe A

§
Urheber: Digitale Lernwelten GmbH auf Basis von Canva
Lege in deinem Heft ein Baumdiagramm zum folgenden Zufallsversuch an. Schreibe die Wahrscheinlichkeiten jeweils als Bruch auf.
Ein nicht gezinkter Würfel wird zwei Mal hintereinander geworfen.
Aufgabe A: Lösung
Aufgabe A: Lösung

§
Aufgabe B
Zeichne in dein Heft ein Baumdiagramm für diesen Versuch und notiere die Wahrscheinlichkeiten als Brüche:
Stell dir vor, du hast eine Urne mit 2 roten (R) und einer schwarzen (S) Kugel. Du ziehst drei Mal eine Kugel daraus, wobei du nach jedem Zug die Kugel wieder zurücklegst.