In diesem Kapitel lernst du, wie die alten Ägypter ihre Tempelbauten geplant haben und was das mit dem Satz des Pythagoras zu tun hat.

§
© Digitale Lernwelten GmbH, erstellt mit Canva
Die Umkehrung von Pythagoras

§
Urheber: Digitale Lernwelten GmbH
Der frisch ernannte Baumeister des Pharaos steht vor der Aufgabe, einen Tempel zu errichten: groß, symmetrisch und mit rechteckigen Grundriss soll er sein. Die rechten Winkel sind entscheidend, um einen eindrucksvollen und vor allem auch stabilen Tempel bauen zu können. Doch wie soll er diese Herausforderung meistern? Da kommt ihm eine Idee - mit einer Zwölfknotenschnur sollte es gehen.
§
Welches Dreieck wurde in Ägypten wohl benutzt, um zu prüfen, ob ein Winkel rechtwinklig ist?
Welches Dreieck wurde in Ägypten wohl benutzt, um zu prüfen, ob ein Winkel rechtwinklig ist?
Um rechte Winkel zu messen, nutzten die alten Ägypter ein spezielles Dreieck mit je 3, 4 und 5 Knoten pro Seite. Nur in dieser Anordnung bildet das Dreieck einen rechten Winkel.
Aufgabe
Begründe, ob die Dreiecke mit den folgenden Seitenlängen rechtwinklig sind.
a) a = 8 cm b = 6 cm c = 10 cm
b) a = 5 cm b = 12 cm c = 15 cm
c) a = 15 cm b = 8 cm c = 17 cm
d) a = 35 cm b = 12 cm c = 37 cm
e) Kann man die nicht rechtwinkligen Dreiecke anpassen, sodass auch sie rechtwinklig sind? Wenn ja, wie?
Aufgabe
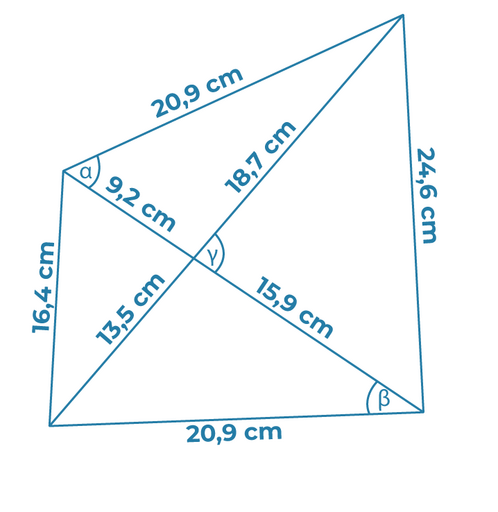
§
Urheber: Digitale Lernwelten GmbH
Wie viele rechte Winkel findest du in der Figur?
Wo sind sie?
Aufgabe
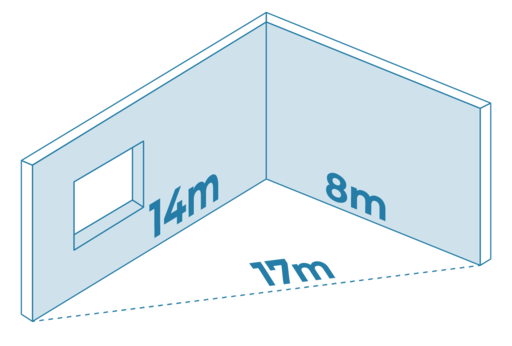
§
Urheber: Digitale Lernwelten GmbH
Stehen die Wände rechtwinklig zueinander?
Begründe deine Antwort rechnerisch.
Aufgabe
Kann man mit einem Seil, das 31 Knoten hat, einen rechten Winkel messen? Begründe deine Antwort.
Wenn deine Antwort „nein“ lautet: wie müsstest du das Seil verändern, damit man damit einen rechten Winkel messen kann?