Übe die Ermittlung von Wahrscheinlichkeiten im letzten Kapitel noch etwas.

§
© Digitale Lernwelten GmbH auf Basis von Canva
Übungen zu Zufallsversuchen
1. Aufgabe

§
© Digitale Lernwelten GmbH auf Basis von Canva
Am Flughafen wird eine fünfköpfige Gruppe zur Zollkontrolle geführt. Alle behaupten, in ihrem USA-Urlaub nur erlaubte Warenwerte eingekauft zu haben, aber Sven und Tim haben tatsächlich den erlaubten Wert überschritten und schmuggeln Waren. Der Zollbeamte entscheidet sich, zwei der fünf Personen zu durchsuchen.
- Wie hoch ist die Wahrscheinlichkeit, dass der Zollbeamte zwei Nicht-Schmuggler (N) erwischt?
- Und wie wahrscheinlich ist es, dass er mindestens einen der beiden Schmuggler (S) findet?
Zeichne zuerst ein Baumdiagramm und berechne dann die Wahrscheinlichkeiten für diese beiden Fälle.
Lösung zur 1. Aufgabe
Lösung zur 1. Aufgabe
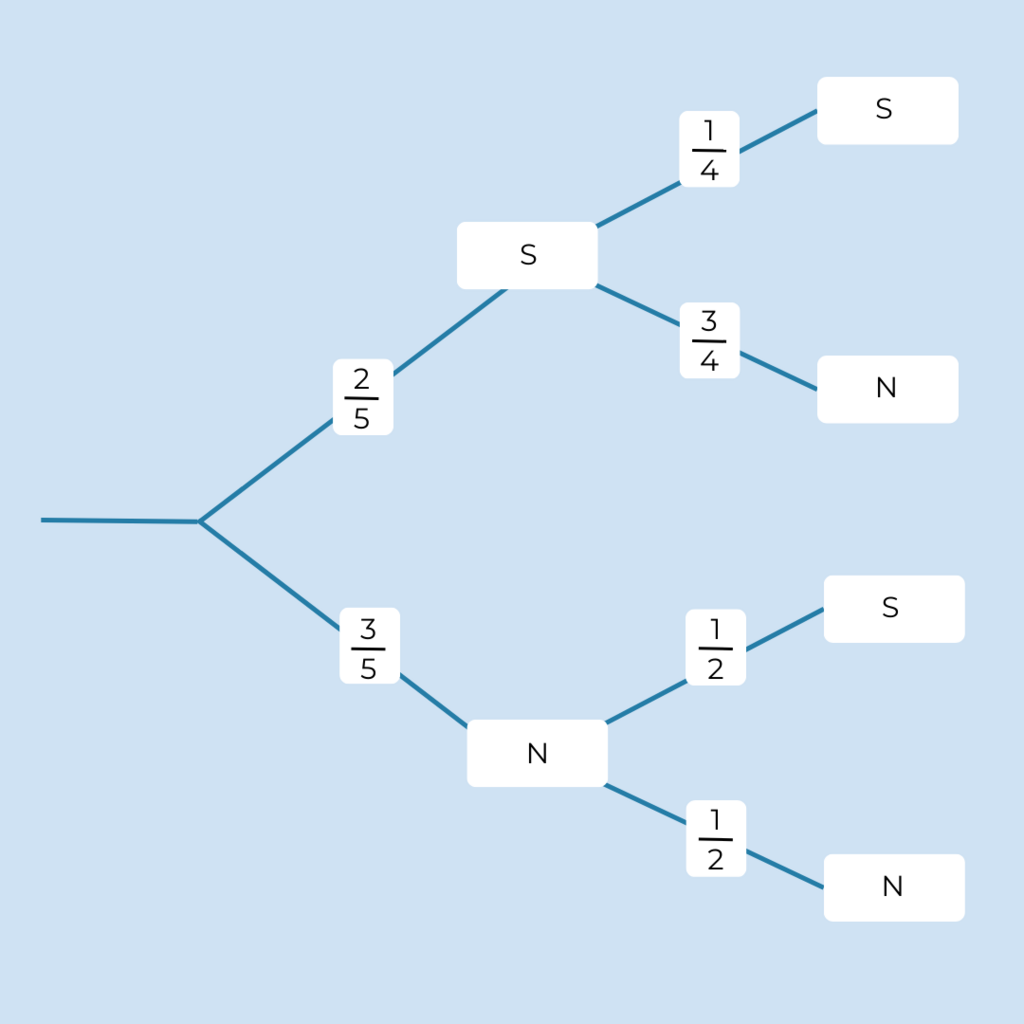
§
Das ist das Baumdiagramm zur Aufgabe.
Folgende Ereignisse sind möglich:
S-S; N-S; S-N; N-N

§
Hier kannst du den jeweiligen Rechenweg nachvollziehen.
2. Aufgabe

§
© Digitale Lernwelten GmbH auf Basis von Canva
Ein Multiple-Choice-Test hat vier Fragen. Jede Frage bietet drei Antwortmöglichkeiten: eine richtige (r) und zwei falsche (f). Eine Person macht den Test ganz ohne Vorbereitung und wählt ihre Antworten zufällig aus.
Wie wahrscheinlich ist es, dass die Person den Test besteht, indem sie mindestens drei von vier Fragen richtig ankreuzt?
Zeichne zuerst ein Baumdiagramm für die vier Fragen und rechne danach aus, mit welcher Wahrscheinlichkeit der Test bestanden wird.
Lösung zur 2. Aufgabe
Lösung zur 2. Aufgabe
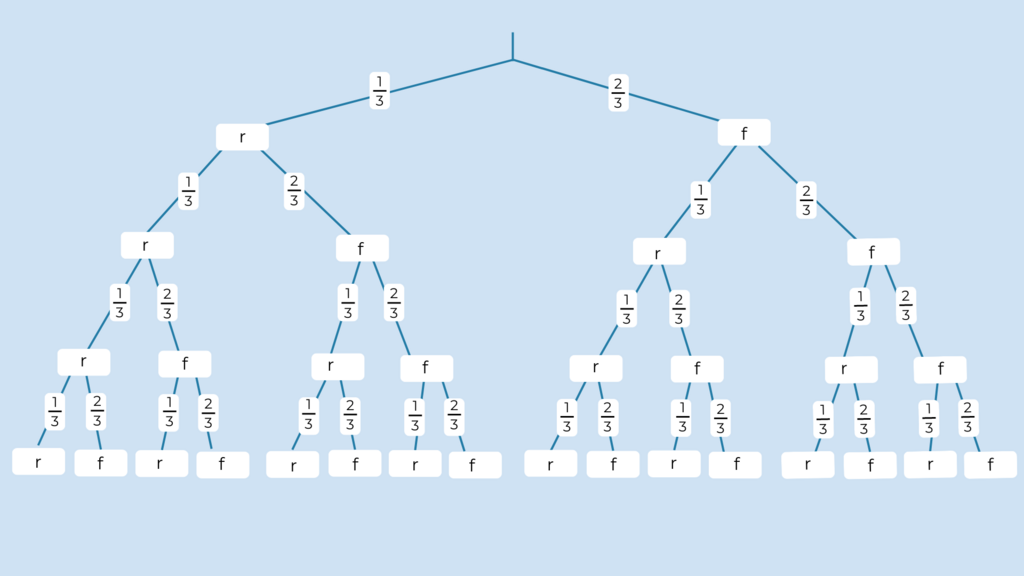
§
So sieht das Baumdiagramm für die Wahrscheinlichkeit des Ergebnisses aus, dass die Person den Test besteht.

§
Hier kannst du den Rechenweg nachvollziehen.
3. Aufgabe

§
© Digitale Lernwelten GmbH
Das Glücksrad rechts wird zweimal gedreht. Beim ersten Dreh notiert man die Zahl, die es anzeigt, und beim zweiten Dreh die Farbe, die ein Feld hat.
- Ist das Glücksrad fair? Denke darüber nach und tausche dich mit deiner Sitznachbarin oder deinem Sitznachbarn aus.
- Wie groß ist die Wahrscheinlichkeit, dass der Pfeil auf die blaue 8 zeigt?
- Und wie wahrscheinlich ist es, dass bei zwei Drehungen eine grüne gerade Zahl herauskommt?
Schreibe alle Wahrscheinlichkeiten als Brüche auf.
Lösung zu 3. Aufgabe
Lösung zu 3. Aufgabe

§
4. Aufgabe

§
© Digitale Lernwelten GmbH
In einer Schüssel liegen vier weiße (W), zehn graue (G) und eine schwarze (S) Kugel. Nacheinander werden zwei Kugeln ohne Zurücklegen gezogen.
- Fertige ein Baumdiagramm für diesen zweistufigen Zufallsversuch an und schreibe an jeden Ast die dazugehörige Wahrscheinlichkeit.
- Berechne, wie wahrscheinlich es ist, dass du nach zweimaligem Ziehen eine graue und eine weiße Kugel erhältst. Schreibe die Wahrscheinlichkeit auch als Prozentzahl auf.
- Berechne auch, wie hoch die Wahrscheinlichkeit ist, dass bei zweimaligem Ziehen mindestens eine Kugel grau ist. Gib auch diese Wahrscheinlichkeit in Prozent an.
Lösung zu 4. Aufgabe
Baumdiagramm
Lösung zu 4. Aufgabe
Baumdiagramm
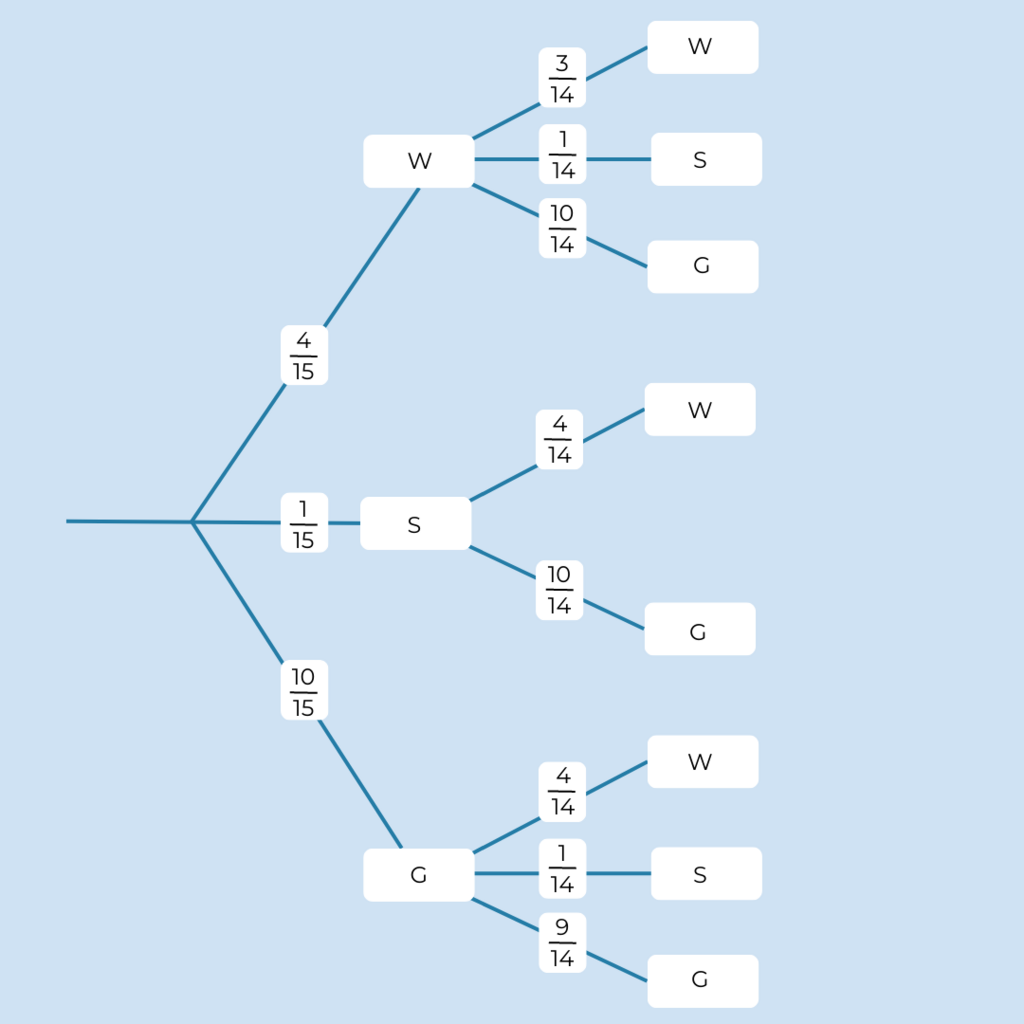
§

§
5. Aufgabe

§
© Digitale Lernwelten GmbH
Nun wiederholst du den Zufallsversuch aus Aufgabe 4, dieses Mal jedoch mit Zurücklegen.
Rechne jetzt aus, wie wahrscheinlich es ist, dass du nach zweimaligem Ziehen zwei Kugeln mit der gleichen Farbe erhältst.
Zeichne auch hier zunächst ein Baumdiagramm, um den Versuch zu veranschaulichen.
Lösung zu 5. Aufgabe
Lösung zu 5. Aufgabe
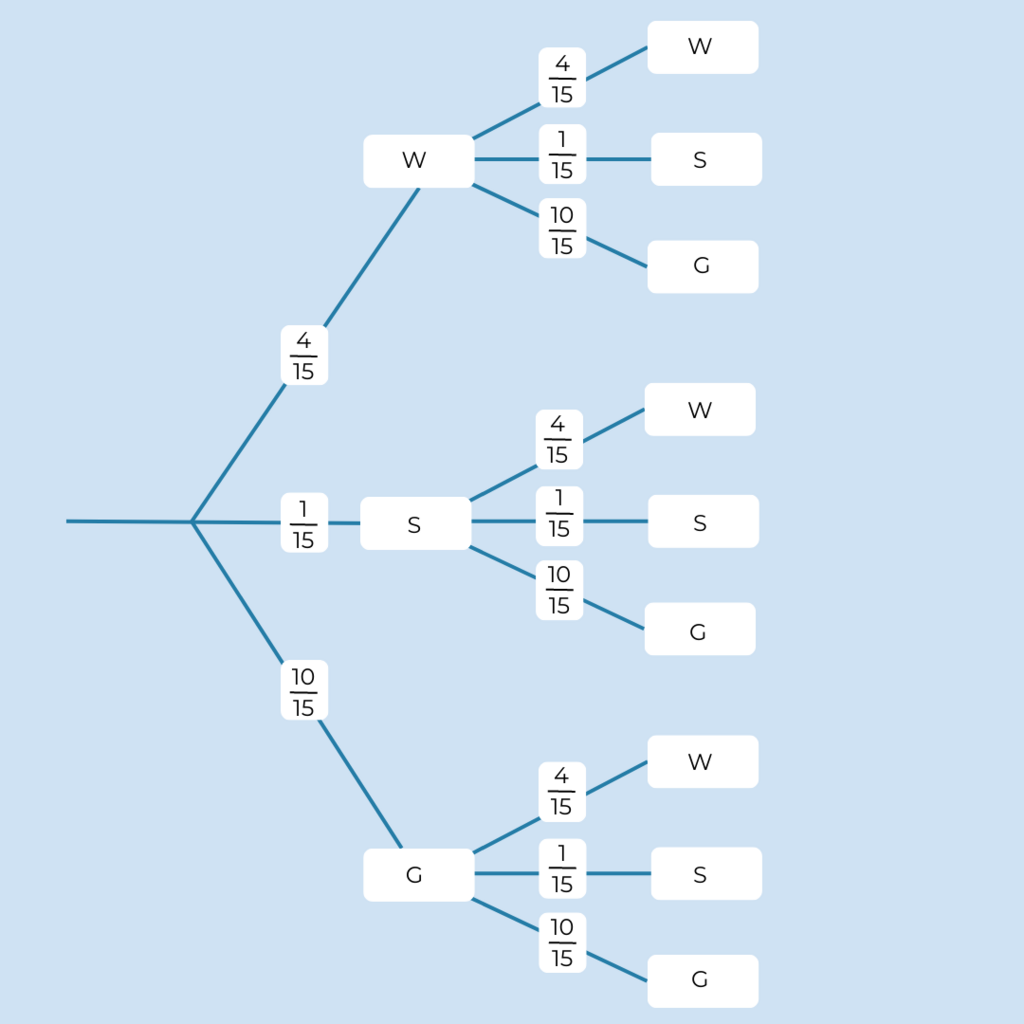
§
So sieht das Baumdiagramm zur 5. Aufgabe aus.
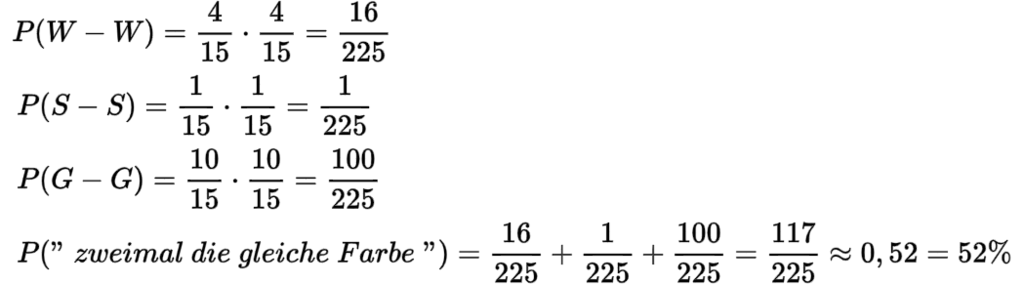
§
Das ist der Rechenweg.