Ähnlich wie Galileo Galilei werden wir eine schiefe Ebene verwenden, um die gleichmäßig beschleunigte Bewegung besser zu verstehen. Das, was wir dabei beobachten, werden wir mithilfe des Experimentierprotokolls systematisch festhalten. Denn unsere heutige Welt wäre eine ganz andere, wenn bedeutende Wissenschaftler ihre Entdeckungen nicht systematisch aufgezeichnet hätten.

§
© Digitale Lernwelten GmbH auf Basis von Canva
Geneigte Ebene und freier Fall
Nach Abschluss dieses Moduls sollst du in der Lage sein ...
Nach Abschluss dieses Moduls sollst du in der Lage sein ...
- ... sorgfältig zu entscheiden, welche experimentellen Daten du auf die passende Art sammeln musst, um eine Bewegung genau zu analysieren.
- ... die Bewegungsgleichungen für gleichmäßig beschleunigte Bewegungen sicher anzuwenden und kinematische Größen in Diagrammen zu interpretieren.
- ... den Unterschied zwischen gleichmäßig beschleunigter und gleichförmiger Bewegung klar zu erkennen.
Die Hypothese
Um die gleichmäßig beschleunigte Bewegung zu untersuchen, verwenden wir eine schiefe Ebene. An deren oberem Ende wird eine Kugel platziert und losgelassen. Entlang der schiefen Ebene sind in regelmäßigen Abständen Glöckchen angebracht, die die Abwärtsbewegung der Kugel „hörbar“ machen.
Aufgabe
Denke darüber nach, was du von diesem Experiment erwartest, und ordne deine Vermutungen entsprechend ein.
Aufbau und Materialliste
In der Animation unten siehst du einen Versuchsaufbau, der sich an den Experimenten von Galileo Galilei orientiert. Alle 0,25 Sekunden hörst du ein Glöckchen klingeln.
Klicke auf „Start“, um die Kugel ins Rollen zu bringen.
§
Urheber: Digitale Lernwelten GmbH
§
Urheber: Digitale Lernwelten GmbH
§
Urheber: Digitale Lernwelten GmbH
Aufgabe
Du kannst diesen Versuch auch in der Realität nachbauen. Ziehe alle Materialien, die du für den Versuch brauchst, nach links und lege diejenigen, die du nicht benötigst, nach rechts.
Versuchsdurchführung
Zu Beginn ist es sinnvoll, dass die Kugel möglichst langsam die geneigte Ebene hinunterrollt. Stelle die Neigung der dafür auf 10° ein.
Wenn du die Glöckchen klingeln hörst, bedeutet das, dass du alles richtig machst. Jedes Mal, wenn du das akustische Signal hörst, wird die Position der Kugel durch einen Spurpunkt festgehalten.
Aufgabe
Bestimme den Weg s (die Entfernung vom Startpunkt), um die vergangene Zeit den jeweiligen Positionen (abgekürzt als „Pos.“; Start ist Pos. 0) zuzuordnen. Trage die Wertepaare in die Tabelle ein.
Versuchsauswertung
In der Tabelle solltest du erkennen können, dass sich der zurückgelegte Weg in gleichen Zeitintervallen immer mehr erhöht. Das zeigt einen deutlichen Unterschied zwischen gleichmäßig beschleunigter Bewegung und gleichförmiger Bewegung. Bei gleichförmiger Bewegung bleibt die Wegänderung in gleichen Zeitabschnitten nämlich gleich.
Aufgabe
Wie du schon weißt, kann es sehr nützlich sein, Messwerte in einem Diagramm zu visualisieren. Trage die Messwerte aus dem obigen Versuch in das Diagramm ein. Messpunkte setzt du, indem du den zweiten Button am oberen Rand des Diagramms anklickst (er zeigt einen blauen Punkt und ein „A“). Anschließend kannst du per Klick in das Diagramm an der entsprechenden Stelle einen neuen Punkt erstellen.
Aktiviere das Häkchen bei „Ausgleichskurve anzeigen“.
Im Diagramm werden die Punkte mit Großbuchstaben beschrieben. Zum Beispiel: Pos. 0 = A, Pos. 1 = B usw.
Du wirst bemerken, dass es hier nicht möglich ist, die Messpunkte mit einer geraden Linie zu verbinden. Das liegt daran, dass es sich nicht um eine gleichförmige Bewegung handelt. Das heißt, in gleichen Zeitabschnitten werden nicht die gleichen Strecken zurückgelegt.
Wir halten fest:

§
© Digitale Lernwelten GmbH
Gegenüberstellung der s(t)-Diagramm für gleichförmige und beschleunigte Bewegung
Im s(t)-Diagramm, das die rollende Kugel auf der 10° geneigten Ebene zeigt, kannst du erkennen, dass der zurückgelegte Weg s quadratisch von der Zeit t abhängt. Es gilt also: s ∼ t². Das ist ein typisches Merkmal einer gleichmäßig beschleunigten Bewegung.
Es gilt die Gleichung s(t) = k * t².
Die Proportionalitätskonstante k kennen wir noch nicht.
Aufgabe
Proportionalitätskonstante k
Ermittle mithilfe des Schiebereglers im Diagramm aus der vorherigen Aufgabe die zum Versuch gehörige Proportionalitätskonstante k. Überlege dir, welche Einheit k haben sollte.
Achtung: Um den Schieberegler zu sehen, musst du das Häkchen bei „Ausgleichskurve anzeigen“ setzen.
Du kannst den Wert für k auch berechnen, indem du für jeden Messpunkt den Quotienten s/t² ausrechnest. Dabei solltest du für jede Position ungefähr denselben Wert erhalten. Daran erkennst du, dass der Weg s in einem quadratischen Verhältnis zur Zeit t steht.
Wichtig: k entspricht dabei nicht der wirkenden Beschleunigung! Es gilt: a = 2 * k. (Hintergrundwissen gibt es im Kasten „für Experten“.)
Allgemein gilt: s(t) = 0,5 * a * t²
Zur Erinnerung:
Bei der gleichförmigen Bewegung gilt s(t) = v * t.
Vertiefung
Herleitung a = g * sin(α)
Vertiefung
Herleitung a = g * sin(α)
Für Experten:
Durch die Zerlegung von Kräften kann man an einer geneigten Ebene ableiten, dass a = g * sin(α) gilt. Dies macht man sich klar, indem man das rechtwinklige Dreieck in der Abbildung betrachtet. Mit Hilfe von trigonometrischen Beziehungen und der Tatsache, dass die Größe einer Kraft F durch F = m * a gegeben ist, ergibt sich durch das Gleichsetzen mit mit FH die oben genannte Formel.
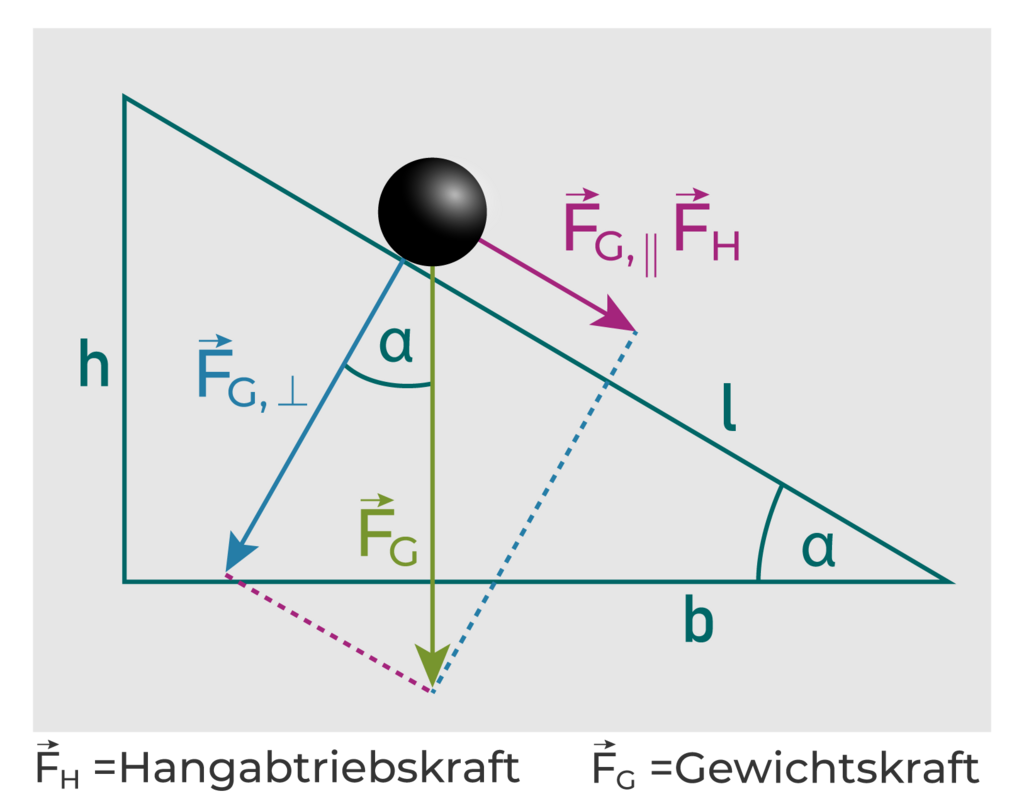
§
Kräftezerlegung an der schiefen Ebene
Überprüfung
Prüfe mithilfe des Taschenrechners nach, ob du mit dieser Formel auch den doppelten Wert von k erhältst.
Näheres wirst du in Jahrgangsstufe 10 lernen. Wenn du jetzt schon mehr wissen willst kannst du dich hier über Kräfte an der schiefen Ebene+ informieren.
Jetzt wissen wir, wie sich der Weg s in Abhängigkeit von der Zeit t bei einer gleichmäßig beschleunigten Bewegung im Vergleich zur gleichförmigen Bewegung verändert. Was wir noch nicht wissen, ist wie das dazugehörige v(t)-Diagramm (Geschwindigkeit-Zeit-Diagramm) aussieht.
In der Animation weiter unten kannst du die Augenblicksgeschwindigkeit der Kugel an den verschiedenen Positionen ablesen.
§
Urheber: Digitale Lernwelten GmbH
§
Urheber: Digitale Lernwelten GmbH
§
Urheber: Digitale Lernwelten GmbH
Aufgabe
Erstelle ein v(t)-Diagramm für die um 10° geneigte Ebene.
Wir halten fest:

§
Urheber: Digitale Lernwelten GmbH
Gegenüberstellung v(t)-Diagramm gleichförmige und beschleunigte Bewegung
Bisher haben wir uns die gleichmäßig beschleunigte Bewegung angesehen, bei der gilt: a(t) = konstant. Daher wäre der Graph im a(t)-Diagramm (Beschleunigung-Zeit-Diagramm) eine Linie parallel zur t-Achse.
Mit Hilfe des a(t)- und des v(t)-Diagramms können wir mehr als nur Aussagen über die zeitliche Veränderung der Beschleunigungs- und Geschwindigkeitsmesswerte machen.
Verwende das nachfolgend GeoGebra-Element, um diesem „Geheimnis“ auf die Spur zu kommen.
Aufgabe
In der Datei werden gleiche Objekte mit gleichen Farben dargestellt. Welche Objekte gehören zusammen?
Aufgabe
Bewege den Schieberegler und beobachte, wie sich dies auf die Diagramme und Gleichungen auswirkt.
Siehst du, dass sich Änderungen immer nur „nach rechts“ auswirken (das heißt, von dem linken Diagramm über das mittlere zum rechten), aber nie umgekehrt „nach links“?
Erkläre, woran das liegt.
Vertiefung
Vertiefung
Veränderung der Startwerte
In der obigen Animation hast du die Möglichkeit, die Anfangswerte zu ändern. Du könntest beispielsweise ein Objekt betrachten, das bereits mit einer Anfangsgeschwindigkeit startet. Beschreibe, welche Effekte diese Veränderungen auf die Bewegung des Objekts haben.
Aufgabe
Erhöhe in der obigen Animation den Winkel auf 30° und anschließend auf 50°. Trage die Messreihen jeweils in ein separates s(t)- und ein v(t)-Diagramm ein.
Vergleiche die Ausgleichskurven und halte deine Beobachtungen fest.
Ein grafikfähiger Taschenrechner, GeoGebra oder ein Tabellenkalkulationsprogramm können dir diese Übung erleichtern.
Galileo Galilei und die geneigte Ebene

§
Urheber: Domenico Tintoretto
https://de.wikipedia.org/wiki/Galileo_Galilei#/media/Datei:Galileo_Galilei_2.jpg
Doch warum hat Galileo Galilei sich so eingehend mit der geneigten Ebene beschäftigt?
Er wollte eigentlich mehr über den freien Fall herausfinden. Aber er hatte nicht die richtigen Geräte, um genau zu messen, wie lange etwas im freien Fall braucht. Es passierte alles zu schnell. Deshalb benutzte er eine schiefe Ebene. Indem er den Winkel der Ebene vergrößerte, konnte er besser verstehen, wie der freie Fall funktioniert. Das war eine richtig kluge Idee! Als „Taktgeber“ für die Markierung der Spurpunkte benutzte Galilei übrigens seinen eigenen Pulsschlag.
Vertiefung
Der Laborbericht von Galileo Galilei
Vertiefung
Der Laborbericht von Galileo Galilei
Beschreibung der Anordnung und Ergebnis:
„Wir verwendeten eine etwa 12 Ellen lange, eine halbe Elle breite und drei Finger breite dicke Planke oder Bohle. An ihrer Schmalseite wurde eine etwa einen Finger breite, vollkommen gerade Rinne eingeschnitten. Diese glätteten und polierten wir und kleideten sie mit möglichst glattem, gut poliertem Pergament aus. In der Rinne ließen wir eine harte, glatte und vollkommen runde Bronzekugel rollen. Wir lagerten das eine Ende ein bis zwei Ellen höher als das andere und ließen, wie ich soeben sagte, entlang der jetzt schief liegenden Rinne die Kugel rollen.
Die zum Abrollen benötigte Zeit stellten wir mithilfe einer noch zu schildernden Methode fest. Diesen Versuch wiederholten wir mehrere Male, um die Messgenauigkeit der Zeit soweit zu erhöhen, dass die Abweichungen zwischen je zwei Beobachtungen nie größer als ein Zehntel Pulsschlag waren. Als dieses vollbracht war und wir uns von der Zuverlässigkeit der Methode überzeugt hatten, ließen wir die Kugel nur den vierten Teil der Gesamtlänge der Rinne durchlaufen; als wir die hierfür nötige Zeitspanne maßen, stellten wir fest, dass sie genau die Hälfte von der im ersten Versuch gemessenen betrug.
Dann untersuchten wir andere Entfernungen und verglichen die zum Durchlaufen der gesamten Länge der Rinne benötigte Zeit mit der für die Hälfte, zwei Drittel, drei Viertel oder einen beliebigen Bruchteil benötigten. Bei diesen Versuchen, die wir alle hundertmal wiederholten, erhielten wir stets das Ergebnis, dass sich die zurückgelegten Strecken wie die Quadrate der Zeiten verhielten*. Das traf für alle Neigungen der Ebene, d. h. der Rinne zu, über die wir die Kugel rollen ließen.
Auch beobachteten wir, dass die Laufzeiten für verschiedene Neigungen der Ebene genau in dem Verhältnis zueinander standen, das der Autor dafür abgeleitet und vorhergesagt hatte ...“
*Hieraus konnte man schließen, dass eine konstant beschleunigte Bewegung vorlag.